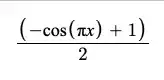How to create variations of a function that have the same start/end point?

Question

I need to create some fake data that sort of conforms to the slow start, randomness in the middle, then a slow finish.

I've screwed around with a graphing calculator and normalized this simple function to start at 0 and end at 1.

How would I go about creating multiple variations of this function (or another function) where Y is always increasing but at different rates?

To be clear, the function should start at 0,0 and end at 1,1 with Y always increasing. I'm looking for a way to programatically create "random-ish" plots.

Answer 1

To elaborate on Joe's comment, I suggest using functions of the form

$$f(x) = \begin{cases} 0 & x \leq a \\ g(\frac{x-a}{b-a}) & a < x < b \\ 1 & x \geq b \end{cases}$$

Where $g(x) = \frac{e^{-\frac{1}{x}}}{e^{-\frac1x}+e^{-\frac1{1-x}}}$

and $a < b$ are chosen randomly between $0$ and $1$.

You can see what these functions (and the corresponding random functions) look like here: https://www.desmos.com/calculator/xdxg1a1hgc

Answer 2

If you want to create a function $f:[0,1]\to[0,1]$ such that:

• $f$ is increasing
• $f(0)=0$
• $f(1)=1$

First you can consider some parametrized families of functions that satisfy those three conditions.

One such family is $f(x)=x^p$ for $p>0$.

Another is $\frac{(2x-1)^{1/p}+1}{2}$ for an odd integer $p$, which has the "slow start" and "slow finish" when $p>1$.

You can choose the value for $p$ randomly according to some distribution.

@TomKern gave you a family with two parameters to choose.

However, depending on how "random" you want it to look, the technique I was suggesting in the comments is to create a convex combination of such functions.

If you have $n$ functions $f_i$ that each satisfy the three conditions, and you have any positive constants: $c_1, c_2, \dots, c_n$, such that they sum to one, then for $0\le x \le 1$, define: $$f(x) = c_1 f_1(x) + c_2 f_2(x) + \dots + c_n f_n(x)$$

• For any $0\le x_1 < x_2 \le 1$, since $f_i(x_1)<f_i(x_2)$ and $c_i>0$, we have that $c_i f_i(x_1)<c_i f_i(x_2)$. Since this is true for all $1\le i \le n$, we have that $f(x_1)<f(x_2)$.
• $c_1 f_1(0) + c_2 f_2(0) + \dots + c_n f_n(0) = 0$
• $c_1 f_1(1) + c_2 f_2(1) + \dots + c_n f_n(1) = c_1 + c_2 + \dots + c_n = 1$

For example, your algorithm could pick three positive values $p_1, p_2, p_3$ according to some discrete distribution on the odd integers, and pick $r_1, r_2, r_3$ independently from a uniform distribution on $(0,1)$. Then, define: $$c_1 = \frac{r_1}{r_1+r_2+r_3}$$ $$c_2 = \frac{r_2}{r_1+r_2+r_3}$$ $$c_3 = \frac{r_3}{r_1+r_2+r_3}$$ $$f(x) = c_1 \frac{(2x-1)^{1/p_1}+1}{2}+ c_2 \frac{(2x-1)^{1/p_2}+1}{2} + c_3 \frac{(2x-1)^{1/p_3}+1}{2}$$

Another neat fact is that function composition preserves the three conditions, which is easily proven:

If we have two functions $f:[0,1]\to[0,1]$ and $g:[0,1]\to[0,1]$ that satisfy all three conditions, then:

• For any $0\le x_1 < x_2 \le 1$, since $0\le f(x_1)<f(x_2) \le 1$, we have that $0\le g(f(x_1)) < g(f(x_2)) \le 1$
• $g(f(0)) = g(0) = 0$
• $g(f(1)) = g(1) = 1$

Therefore, after creating $M$ functions using the convex combination technique described above, and labeling them $1, \dots, M$, you could choose a random permutation of the integers $1, \dots, M$; then compose all $M$ functions in that order.