1

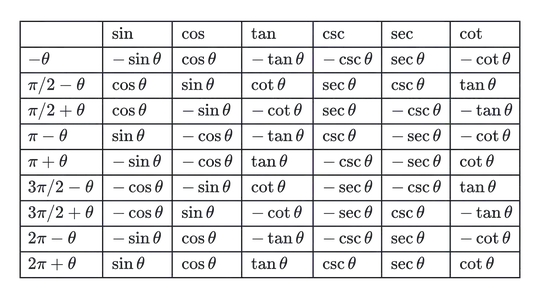
Trigonometry allied angles I have proved the table given above, for example, $\cos \left( \dfrac{\pi }{2}-\theta \right) =\sin \theta $ and $\cos \left( \dfrac{\pi }{2}+\theta \right) =-\sin \theta $ using sum/difference identities, but I need intuition (using unit circle/right triangle/graphs, etc.) for understanding and remembering the same. I need Intuition for understanding and remembering the reflections/symmetry, shifts, parity, and periodicity of sine and cosine functions at allied angles 0, $π/2$, $π$, $3π/2$, and $2π$.

  • All you need to remember is $\sin$ and $\cos$. Rest follows. Cos is negative in second and third quadrant as $x$ is negative and Sin is negative in third and fourth quadrant as $y$ is negative. – Math Lover Jul 26 '21 at 14:52
  • 1
    Etymologically, cosine means "sine of the complementary angle", and so $\cos(\theta)=\sin(\pi/2-\theta)$. You can also understand this identity by considering graph transformations: if $g(x)=f(\pi/2-x)$ for all $x$, then $g(\pi/2-x)=f(x)$, and so each point $(x,f(x))$ that lies on the graph of $f$ is mapped to $(\pi/2-x,f(x))$—a reflection in the vertical axis followed by a horizontal shift of $\pi/2$ units to the right. – Joe Jul 26 '21 at 15:31
  • Related (duplicate?): "How to remember a particular class of trig identities.". See, in particular, my answer. – Blue Jul 26 '21 at 17:37

0 Answers0