0

Problem: prove that $ \int_{-\infty}^\infty \frac{1-\cos(ax)}{x^2} \, dx = \pi|a|$

My thoughts: we can try integration by parts

$$\int \frac{1-\cos (ax)}{x^2} = (\cos (ax) -1) \,d \frac{1}{x} = \frac{(\cos (ax) -1)}{x} - \int \frac{1}{x} \,d (\cos (ax) -1) = \frac{(\cos (ax) -1)}{x} + \int \frac{\sin(ax)}{x} \, dx $$

It looks a lot nicer and I think I am getting close...

Michael Hardy
  • 1
R.Yeh
  • 173
  • 5
  • See here for some solutions. Of course you could insist on finishing your approach, but I suppose it's good to have alternate solutions as well. – Sarvesh Ravichandran Iyer Jul 26 '21 at 00:54
  • I think the best approach from here would probably be to solve the last sinc-like integral using residues, I'm sure there's a way to do it without complex analysis but the residue method seems pretty straightforward – Stephen Donovan Jul 26 '21 at 00:57
  • 3
    $$ \begin{align} & \int_{-\infty}^{+\infty} \frac{1-\cos(ax)}{x^2} ,dx \ {} \ = {} & a\int_{-\infty}^{+\infty} \frac{1-\cos(ax)}{(ax)^2} (a,dx) \ {} \ = {} & a\int_{\mp\infty}^{\pm\infty} \frac{1-\cos u}{u^2}, du \ {} \ = {} & |a| \int_{-\infty}^{+\infty} \frac{1-\cos u}{u^2}, du \end{align} $$ So the question is how to show that $$ \int_{-\infty}^{+\infty} \frac{1-\cos u}{u^2},du = \pi. $$ – Michael Hardy Jul 26 '21 at 02:50

1 Answers1

5

Let $$f(z) = \frac{1-e^{|a|iz}}{z^2}$$

and let the contour $C$ be $$ C = \Gamma_1 \cup \gamma_0 \cup \Gamma_2 \cup \Gamma_R$$

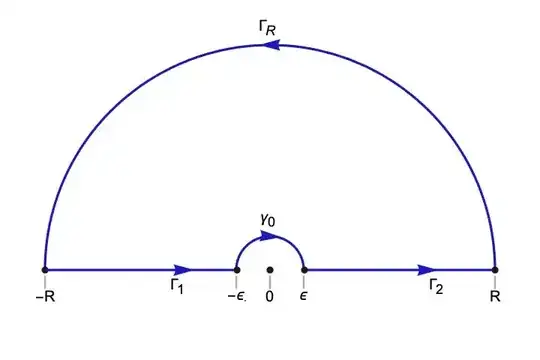
enter image description here

Consider $$\lim_{\epsilon\to0}\oint_C f(z) \, dz = -\pi i \,\text{res}_{z=0} f(z)$$

$$\begin{aligned} \int_C f(z)\, dz &= \int_{\Gamma_1}f(z)\,dz+\int_{\gamma_0}f(z)\,dz+\int_{\Gamma_2}f(z)\,dz+\int_{\Gamma_R}f(z)\,dz\\ &= \int_{-R}^{-\epsilon} \frac{1-\cos ax}{x^2}\,dx+\int_{\epsilon}^{R} \frac{1-\cos ax}{x^2}\,dx \\ & -i\int_{-R}^{-\epsilon}\frac{\sin |a|x}{x^2}\,dx-i\int_{\epsilon}^R\frac{\sin |a|x}{x^2}\,dx +\int_{\gamma_0} f(z)\,dz + \int_{\Gamma_R} f(z)\,dz\end{aligned}$$

The integrand of the third and fourth integrals is odd, so that the sum of these integrals is zero. The integral of $\Gamma_R$ can be bounded as follows:

$$\left|\int_{\Gamma_R} f(z) \,dz \right|\le \int_{0}^\pi \left| \frac{1+e^{-|a|R\sin\theta}}{R^2} \,R\,\right| d\theta < 2\int_{0}^{\pi/2} \left| \frac{1+e^{-\frac{2|a|R \theta}{\pi}}}{R^2} \,R\,\right| d\theta<\frac{2\pi}{R} \to 0, \text{ as } R\to \infty.%\quad (\text{for }\theta>0, 1+e^{-\frac{|a|R\theta}{2}}<2)%$$

So, let $R\to \infty$ and $\epsilon \to 0$, and

$$\displaystyle \int_{-\infty}^\infty \frac{1-\cos a x}{x^2} = \pi i \, \text{res}_{z=0} \frac{1 - e^{|a|iz}}{z^2}= -\pi i \, \text{res}_{z=0} \frac{|a|iz + \frac{(|a|i z)^2}{2!}+\frac{(|a|i z)^3}{3!}+\cdots}{z^2}=\pi |a|$$

mjw
  • 8,647
  • 1
  • 8
  • 23
  • I'm new to contour integration. Where do the third and fourth integrals come from? – Joey Jul 27 '21 at 03:06
  • Hi @Joey, on the real axis, $\displaystyle\frac{1-e^{i|a|z}}{z^2} = \frac{1-e^{i|a|x}}{x^2} = \frac{1-\cos a x - i \sin |a| x}{x^2}.$ – mjw Jul 27 '21 at 03:11
  • Okay thank you. How did you get the second inequality? For the estimation for $\Gamma_R$ integral. I guess $\sin \theta < \theta$ for $\theta \in (0, \infty)$ but not sure if that gives it. – Joey Jul 27 '21 at 04:01
  • 1
    $\sin \theta > \frac{\theta}{2}$ when $0<\theta \le \frac{\pi}{2}$ – mjw Jul 27 '21 at 05:11
  • 1
    https://mathworld.wolfram.com/JordansLemma.html – mjw Jul 27 '21 at 05:14
  • Thank you. I understand the whole solution now. – Joey Jul 27 '21 at 06:42