Understanding geometrical intuition behind $\frac{d}{d\theta}\sin(\theta)$ from 3b1b video

Question

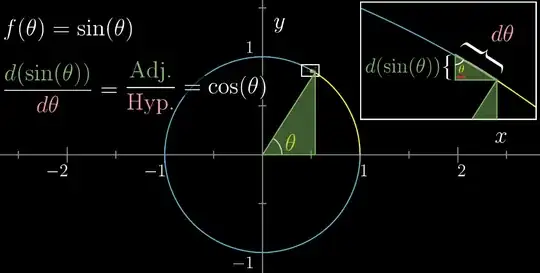
I was going through this 3b1b video on obtaining derivative formula through geometrical intuition. While discussing how to obtain $\frac{d}{d\theta}\sin(\theta)$, Grant draws following diagram:

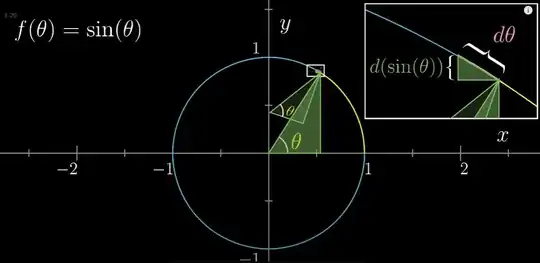
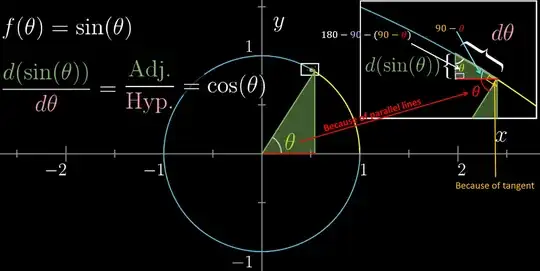
I did not understand how the angle inside the smaller triangle (red underlined at top right corner) formed by $d\theta$ is also $\theta$. Grant also does not seem to have discussed the same in the video. He only showed the animation equating the two angles of smaller and larger triangle:

What I am missing here?

Answer 1

The base of the small triangle is parallel to the base of the large triangle, so the angle between the hypotenuse of the large triangle and the base of the small triangle is $\theta$.

From there, presuming this portion of the circle "straightens out" as you zoom in, the angle between the base of the small triangle and its hypotenuse must be $90 - \theta$ so that the two angles add up to $90$ degrees.

You now have a triangle with a right angle, and an angle of $90-\theta$. To achieve a sum of $180$ degrees, the remaining angle will be $\theta$ as shown in the diagram.