0

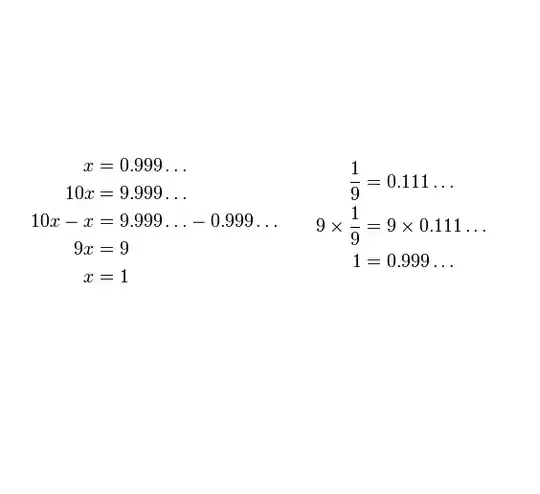
What is the mistake in balancing this equation? It says $.99999 = 1$, in step 3 $x$ is subtracted from the left side and $.99999$ from the right side. Shouldn't that mean there is some division by $0$ stopping the equation from being right?

Equation

Blue
  • 75,673
arclengths
  • 61
  • 5
    I don't see an issue: nowhere it's being stated that $0.99999=1$; these are all valid manipulations around the true statement that $0.\overline 9=1$. –  Jul 20 '21 at 12:27
  • 3
    https://en.wikipedia.org/wiki/0.999... – Steven01123581321 Jul 20 '21 at 12:27
  • In this proof that $1=2$, $a$ can't equal $b$, does the same thing happen in this proof $1$ equals $.9$ repeating? https://www.youtube.com/watch?v=hI9CaQD7P6I – arclengths Jul 20 '21 at 12:30
  • 3
    @arclengths, the fatal mistake in the youtube "proof" that $1=2$ comes when the factor $(a-b)$ is cancelled from both sides of the equation $(a+b)(a-b)=b(a-b)$, because $a-b=0$. In the proof here, the factor being cancelled is $9$, and $9$ is not equal to $0$, so the cancellation is OK. – Barry Cipra Jul 20 '21 at 14:33
  • I agree with the posts in the linked question that this approach to proving the equality of $0.9999\dots$ and $1$ is invalid as it makes assumptions as to the allowed operations when manipulating these infinite expressions or makes a circular argument as manipulating $\frac{1}{3}=0.3333\dots$ or $\frac{1}{9}=0.11111\dots$ which if the initial identity is in question then these other identities should also be questioned. – JMoravitz Jul 20 '21 at 16:25

1 Answers1

0

There is no mistake in these proofs. Both of them are completely valid and proof that $1 = 0.9999\dots$. This statement is, indeed, true. This can be sometimes confusing to people and it's completely normal that it feels weird at first.

If you think about it in the following way, it might make sense: What would $1-0.9999\dots$ be? The difference between these two numbers is smaller then any rational number. The only number that is smaller than any other is $0$. Thus: $1-0.9999\dots = 0$, which implies $1 = 0.9999\dots$.

Guenterino
  • 860
  • 4
  • 17