7

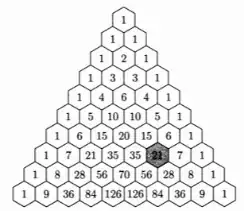
Consider the hexed version of Pascal's triangle shown in the figure here:enter image description here

Note further that the shaded entry $21$ on the right side is surrounded by six numbers: $6$, $15$, $35$, $56$, $28$, $7$. Note further that$$6 \times 35 \times 28 = 15 \times 56 \times 7.$$Will this pattern hold for any number we choose in the triangle? Prove that it does or find a counterexample.

The question is asking if we have the equality$$\binom{n-1}{k}\binom{n}{k-1}\binom{n+1}{k+1} = \binom{n-1}{k-1}\binom{n}{k+1}\binom{n+1}{k}$$Expanding we get$${{(n-1)!}\over{k!(n-k-1)!}} {{n!}\over{(k-1)!(n-k+1)!}} {{(n+1)!}\over{(k+1)!(n-k)!}} = {{(n-1)!}\over{(k-1)!(n-k)!}} {{n!}\over{(k+1)!(n-k-1)!}} {{(n+1)!}\over{k!(n-k+1)!}}$$Cancelling like terms on both sides it's clear the equality follows.

However, this was not a combinatorial proof. I was wondering if someone can give me a hint (NOT A COMPLETE SOLUTION) towards a combinatorial proof of this equality? My thoughts are to show an equality between $2$ ways to count certain types of paths that pass through $2$ specific fixed points (that aren't the starting point nor the endpoint) in a $n \times n \times n$ grid.

Will Orrick
  • 18,220
Emperor Concerto
  • 1,415
  • 2
    +1 : I know that I am supposed to silently upvote, but in addition to being an interesting question, you have presented the question very elegantly. – user2661923 Jul 18 '21 at 23:53
  • 2
    Duplicate of https://math.stackexchange.com/questions/20749/the-hexagonal-property-of-pascals-triangle, yes? As far as I can tell, this is one of those frustrating simple identities where the combinatorial proof remains elusive. – Mike Earnest Jul 18 '21 at 23:53
  • 2
    That duplicate was also re-asked on MathOverflow and Theo Johnson-Freyd gave a nice answer there. – Will Orrick Jul 19 '21 at 05:23

0 Answers0