1

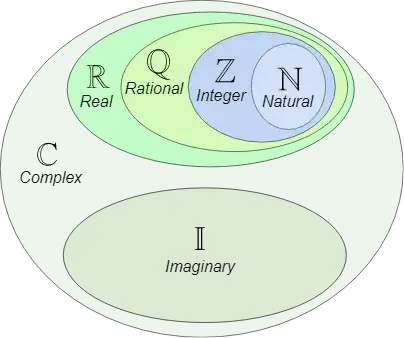
enter image description here

This image makes it seem like real and imaginary numbers are all complex numbers. I thought complex numbers were numbers composed of a real and imaginary part. This got me thinking, and I think I might see it now. All real numbers can be written as $$r \times i^{4k}$$ and all imaginary numbers can be written as $$i^k \times 1$$ or $$i^k + 0$$ There are other ways to combine them in ways that does nothing to the value. So, is it these combinations that make all real and imaginary numbers into complex numbers?

A. Kvåle
  • 323
  • 1
  • 12
  • 3
    A number is complex , if it can be written as $a+bi$ with real numbers $a,b$. So , yes, a complex number can be purely imaginary and also real. And every real number as well as every purely imgainary number is complex. For the real numbers we just set $b=0$ and for the purely imgainary numbers we set $a=0$ to get the desiresd representation. – Peter Jul 18 '21 at 15:45
  • This is a more complicated question than you realize. Far simpler question... "Is the natural number $1$ equal to the integer number $1$?" As sets? No, they are not equal. The natural number $1$ is equal to ${\emptyset}$ if defined via Von Neumann's construction of the naturals while the integer $1$ is ${(1,0),(2,1),(3,2),(4,3),(5,4),\dots}$ (where the numbers appearing are the natural numbers). Despite this, there is a very clear association between the natural number $1$ and the integer $1$ and we often gloss over the distinction and freely switch between them at will. – JMoravitz Jul 18 '21 at 15:57
  • 1
    So... it is more correct to say that the complex numbers contains a subset which is isomorphic to the reals... and if we refer to a number such as $1$, it could just as well have been referring to the complex number $1$, the real number $1$, the rational $1$, or whichever other that we wanted... The process of switching between them is so second nature and glossed over so heavily that many people do it without thinking and many ley persons aren't aware of it at all in the first place. – JMoravitz Jul 18 '21 at 16:00
  • TLDR: The reals might as well be considered complex numbers. – JMoravitz Jul 18 '21 at 16:01
  • 1
    Does this answer your question? Set Theoretic Definition of Numbers – JMoravitz Jul 18 '21 at 16:03
  • @JMoravitz I think I understand what you're saying: the natural number 1 is not the same as the integer number 1, because the integer version can just written as $1$, or $1 + 0$ or $1 \times 1$, but the natural number 1 can also be written as $0.5 + 0.5$ or $1.5 - 0.5$ and so on? They have infinitely many different ways of being written, but depending on what set they exist in, the possible ways differ. – A. Kvåle Jul 18 '21 at 16:06
  • 1
    No, the number or types of different representations is irrelevant. The base formal definition is what matters here if you want to talk about true equality. If you want to talk about informal equality, then as alluded to earlier... we often say that the natural number $1$ is (informally) "equal" to the integer $1$. As for the natural being written as $0.5+0.5$... I would not have allowed that... since if we were working purely in the context of naturals you have $0.5$ is not defined. That is a rational number (or real or higher), not a natural number. – JMoravitz Jul 18 '21 at 16:08
  • @JMoravitz Aha I see, I'll have to read up on some set theory then to understand. – A. Kvåle Jul 18 '21 at 16:10
  • @JMoravitz I didn't see the change in your comment until now. I mixed up some of the sets, as natural numbers are all positive integers (sometimes including 0, sometimes not), and integers are all negative and positive integers (plus 0). For some reason I mixed up natural with rational however. I think you got my misunderstanding though, as 0.5 + 0.5 is a representation of 1 if rational numbers are permissible to use. – A. Kvåle Jul 18 '21 at 17:05
  • It would make me happy to just eliminate the blob with $\mathbb I$ altogether. – rschwieb Jul 18 '21 at 18:28

2 Answers2

3

Perhaps we could modify the Venn diagram to let $\mathbb I$ intersect with $\mathbb Z$ (and consequently $\mathbb R$). (Which integer can be considered imaginary? Which imaginary number can be considered an integer?)

rschwieb: It would make me happy to just eliminate the blob with altogether. $\quad$ Yes that’s true, actually; the set of prime numbers is arguably more deserving of being singled out in this Venn diagram.

And yes, I would certainly classify all real and imaginary numbers as complex; the complex plane includes both the real and imaginary axes, after all.

P.S. I’d never encountered the symbol $\mathbb I$ (which here denotes the set of imaginary numbers) prior to this, but apparently, in the days of yore, it sometimes denoted the set of integers...

ryang
  • 38,879
  • 14
  • 81
  • 179
0

The actual fact of the matter is that different definitions can lead to different answers on whether the real numbers are complex numbers. (In case you’ve never worried about definitions before, then…What, exactly, is a real number, anyway? A complex number?)

What is most important is that, no matter what your answer to that question is, one can always see the real numbers inside the complex numbers by associating the real numbers $a$ to the complex number $a+0i.$ The possibility of such an association, which is the same as looking at the “copy” of the usual number line given by the real axis in the complex plane, is the only issue at hand that has serious mathematician significance, not whether real numbers literally are complex numbers, or are something quite different.

Kevin Carlson
  • 52,457
  • 4
  • 59
  • 113