7

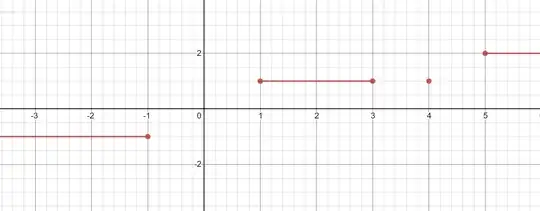
One criterion for checking existence of limits is to check that and one-sided limits from left and right exist and agree:

(Theorem) Let $f$ be a real-valued function. One-sided limits of $f$ as $x$ approaches $a$ from the left and right exist and equal $L$: $$ \lim_{x \to a^-} f(x) = \lim_{x \to a^+} f(x) = L $$ if and only if the two-sided limit of $f$ at $a$ exists and also equals $L$, $$\lim_{x \to a} f(x) = L.$$

The contrapositive of this statement can be used to conclude that a limit does not exist:

(Contrapositive) Let $f$ be a real-valued function. One-sided limits of $f$ as $x$ approaches $a$ from the left and right do not exist or do not agree if and only if the limit of $f$ at $a$ does not exist.

When applying this to a variety of contexts, you can come up with some pretty weird examples and weird results.

enter image description here

In the above figure, it seems to me that

  • $\lim_{x \to 3} f(x)$ does not exist since $\lim_{x \to 3^+} f(x)$ does not exist.
  • $\lim_{x \to 4} f(x)$ does not exist since $\lim_{x \to 4^-} f(x)$ and $\lim_{x \to 4^-} f(x)$ do not exist.
  • $\lim_{x \to 5} f(x)$ does not exist since $\lim_{x \to 5^-} f(x)$ does not exist.

A bit more controversial is if you apply the same to the limits at infinity, which would stand to reason that

  • $\lim_{x \to \infty} f(x)$ does not exist since $\lim_{x \to \infty^+} f(x)$ does not exist.
  • $\lim_{x \to -\infty} f(x)$ does not exist since $\lim_{x \to \infty^-} f(x)$ does not exist.

However to contradict the above, many people would write $\lim_{x \to \infty} f(x)=2$ and $\lim_{x \to -\infty} f(x)=-1$.

TLDR; why does the nonexistence of left and right limits not cause limits at infinity to be undefined but does cause the limit at $x=3$, $x=4$, and $x=5$ to not exist? Real analysis answers are welcome.

Edit Thanks to answers from Troposphere and Joe, I worked out some more careful definitions and theorems:

Definition (Limit) Let $f$ be a function whose domain is a subset of $\mathbb{R}$, and let $a, L \in \mathbb{R}$. We say that the limit of $f$ as $x$ approaches $a$ is $L$, \begin{equation*} \lim_{x \to a} f(x)=L \end{equation*} to mean that $a$ is an accumulation point of $\textrm{dom}(f)$ and for any $\epsilon > 0$, there exists $\delta >0$ such that if $x \in \textrm{dom}(f)$ is within $\delta$ of $a$ (with $x \ne a$), then $f(x)$ is within $\epsilon$ of $L$: \begin{equation*} 0 < |x-a| < \delta \quad \rightarrow \quad 0 < |f(x)-L| < \epsilon. \end{equation*}

Definition (One-Sided Limits) Let $f$ be a function whose domain is a subset of $\mathbb{R}$, and let $a, L \in \mathbb{R}$.:

  • We say the limit of $f$ as $x$ approaches $a$ from the left is $L$, $$\lim_{x \to a^-} f(x)=L,$$ to mean that $a$ is an accumulation point of $\textrm{dom}(f) \cap (-\infty,a]$ and for any $\epsilon > 0$, there exists $\delta >0$ such that if $x$ is within $\delta$ of $a$ (for $x < a$), then $f(x)$ is within $\epsilon$ of $L$: \begin{equation*} 0 < a-x < \delta \quad \rightarrow \quad 0 < |f(x)-L| < \epsilon. \end{equation*}

  • We say the limit of $f$ as $x$ approaches $a$ from the right is $L$, \begin{equation*} \lim_{x \to a^+} f(x)=L, \end{equation*} to mean that $a$ is an accumulation point of $\textrm{dom}(f) \cap [a,\infty)$ and for any $\epsilon > 0$, there exists $\delta >0$ such that if $x$ is within $\delta$ of $a$ (for $x > a$), then $f(x)$ is within $\epsilon$ of $L$: \begin{equation*} 0 < x-a < \delta \quad \rightarrow \quad 0 < |f(x)-L| < \epsilon. \end{equation*}

Theorem (One-Sided and Two-Sided Limits Relationship) Let $f$ be a function whose domain is a subset of $\mathbb{R}$, and let $a, L \in \mathbb{R}$. Suppose a is an accumulation point of dom(f) and that $f$ is defined everywhere in some punctured neighborhood of $a$. Then

One sided limits of $f$ from left and right at $a$ exist and equal $L$, $$\lim_{x \to a^-} f(x) = L \textrm{ and }\lim_{x \to a^+} f(x) = L,$$

if and only if the two-sided limit of $f$ at $a$ exists and also equals $L$: $$\lim_{x \to a} f(x) = L.$$

Contrapositive (One-Sided and Two-Sided Limits Relationship) Let $f$ be a function whose domain is a subset of $\mathbb{R}$, and let $a, L \in \mathbb{R}$. Suppose a is an accumulation point of dom(f) and that $f$ is defined everywhere in some punctured neighborhood of $a$. Then

At least one of the one sided limits of $f$ from left and right at $a$ does not exist or do not equal $L$: $$\lim_{x \to a^-} f(x) \ne L \textrm{ or }\lim_{x \to a^+} f(x) \ne L,$$

if and only if the two-sided limit of $f$ at $a$ does not exist or does not equal $L$: $$\lim_{x \to a} f(x) \ne L.$$

Under these definitions and theorems, I think (hope) we get the conclusions we expect:

  • $\lim_{x \to 3} f(x)$ exists
  • $\lim_{x \to 5} f(x)$ exists.

and

  • $\lim_{x \to 3^+} f(x)$ DNE.
  • $\lim_{x \to 4} f(x)$ DNE.
  • $\lim_{x \to 5^-} f(x)$ DNE.
EthanAlvaree
  • 3,412
  • 9
    Because a limit at infinity has its own definition. Intuitively, you can't treat $\infty$ like a real number, and of course you can only approach $\infty$ from below. But if you want a rigorous explanation, just take a look at how the limit when $x\to\infty$ is defined. – Mark Jul 14 '21 at 20:06
  • Sure! If you can share a rigorous definition from real analysis and compare/contrast with what's happening at an endpoint of a domain (like $x=3$) or singleton point (like $x=4$) I will accept it as an answer! – EthanAlvaree Jul 14 '21 at 20:32
  • Look at the function on $[1,3]$ for example, then $\lim_{x\to 3^+}f(x)$ doesn't make sense because there's nothing right of $3$ so the limit actually becomes the left limit, similarly with $\infty$, there's nothing right to infinity so the limit equals the left limit. – kingW3 Jul 15 '21 at 23:47
  • Perhaps you can use the special case, like Mark said, of the epsilon delta definition for plus or minus infinity to prove whether it is undefined or not. – Тyma Gaidash Jul 17 '21 at 22:55

2 Answers2

8

The general concept of "limit" is more fundamental than "one-sided limit", and the theorem you quote is specifically not a definition of $\lim_{x\to a}$.

In particular, the theorem strictly speaking has some hidden premises that are not clearly shown in the formulation you quote, namely that

  1. $a$ is a real number, and
  2. $f$ is defined everywhere in some punctured neighborhood of $a$ (in $\mathbb R$).

Your conclusions don't work because the first hidden premise fails to hold in the $\infty$ cases, and the second hidden premise fails to hold in the $a\to3,4,5$ cases.

The general concept of limit can be defined* whenever the domain of the function is (a subset of) a topological space, and the $a$ in $x\to a$ is an accumulation point of the domain of the function in question.

For your example this means that limits as $x\to 3$ and $x\to 5$ make sense (and exist), but a limit as $x\to 4$ does not make sense, because $4$ is not an accumulation point of the domain. To speak about limits as $x\to\infty$ or $x\to-\infty$ we can take the underlying topological space to be the extended real line.

*namely: If $X$ and $Y$ are topological spaces, $Z$ is a (not necessarily proper) subset of $X$, $f$ is a function $Z\to Y$, $a$ is an accumulation point of $Z$, and $b\in Y$, we say that $b=\lim_{x\to a} f(x)$ iff:

For every neighborhood $B$ of $b$ in $Y$, there is a neighborhood $A$ of $a$ in $X$ such that for all $x\in (A\cap Z)\setminus\{a\}$ it holds that $f(x)\in B$.

(It's an instructive exercise to verify that this is equivalent to the usual $\varepsilon$-$\delta$ definition of limit in the special case where $X$ and $Y$ are metric spaces rather than merely topological spaces, and $Z$ includes a punctured neighborhood of $a$).

One practical reason to downplay the concept of one-sided limits is that it doesn't generalize well to higher dimensions. For example, if we take $$ f(x,y) = \frac{xy^2}{x^2+y^4} $$ defined on $\mathbb R^2\setminus\{(0,0)\}$, then $\lim_{h\to 0^+}f(hp,hq)=0$ for every $(p,q)\ne(0,0)$ -- that is, no matter which direction we approach $(0,0)$ from, the "single-directional limit" of $f$ exists and is $0$ -- yet $\lim_{(x,y)\to(0,0)}f(x,y)$ does not exist!

Troposphere
  • 7,158
  • 1
    I believe that, according to the more general definition of a limit, if $f(x)$ is not defined for $x\geqslant a$, and $\lim_{x \to a^-}f(x)=l$, then we can say that $\lim_{x \to a}f(x)=l$, as $a$ is still an accumulation point of the domain of $f$, and we are only interested in the behaviour of the function where it is defined. Is that correct? – Joe Jul 14 '21 at 21:55
  • @Joe: Yes, that is true for about definition I've written (and to the best of my knowledge it matches how the word is actually used in practice). – Troposphere Jul 14 '21 at 22:01
  • Thanks for clarifying. I think the problem is that according to the more elementary definition of a limit, we only say that $\lim_{x \to a}f(x)=l$ if $f$ is defined in a punctured neighbourhood of $a$. I believe that this is discussed briefly in Spivak's Calculus. Let me have a look. – Joe Jul 14 '21 at 22:03
  • See here. It's page 105. – Joe Jul 14 '21 at 22:04
  • 1
    @Joe, agreed, which is why I identified it as one of the unspoken assumptions of the OPs result. (Strictly speaking it would have been enough to require that $a$ is an accumulation point of $\operatorname{Dom} f \cap [a,\infty)$ and of $\operatorname{Dom} f \cap (-\infty,a]$ separately, but that's not generally the thing beginner textbooks actually tacitly assume). – Troposphere Jul 14 '21 at 22:09
  • Thank you very much for your thoughtful reply! To clarify, are the limits at $x=3$ and $x=5$ in my example existent or nonexistent? The screenshot from Joe says the function need only exist within some $\delta>0$ of $a$, but not on both sides of $a$. On the other hand, the theorem I cited states the limit from both sides must exist. – EthanAlvaree Jul 15 '21 at 07:07
  • 1
    @EthanAlvaree: The screenshot I've included actually implies that in order for $\lim_{x \to a}f(x)$ to be defined, the function $f$ must be defined on both sides of $a$. More precisely, there has to be a $\delta>0$ such that $f$ is defined on the interval $(a-\delta,a+\delta)$ (except possibly at $a$ itself). According to this definition, the limits at $x=3$ and $x=5$ do not exist. However, if we use the more advanced definition of a limit mentioned in Troposphere's answer, then they do exist. – Joe Jul 15 '21 at 14:08
  • @EthanAlvaree: So the theorem that you cite is perfectly valid according to the elementary definition of a limit, but not according to the advanced definition of a limit, unless we include further hypotheses. – Joe Jul 15 '21 at 14:11
  • Thank you @Joe and @Troposphere! I am still having a hard time believing the limit exists at $x=3$ and $x=5$. I took a look at the "advanced" topological definition of a limit Troposphere mentioned, and it seems to require that $a$ be an interior point, e.g. the set containing $a$ be an open set (or "neighborhood"), but $(3-\delta, 3]$ is not open. Topological definition I am referring to: https://en.wikipedia.org/wiki/Limit_of_a_function#Functions_on_topological_spaces – EthanAlvaree Jul 15 '21 at 17:08
  • 2
    @EthanAlvaree: Yes, $(3-\delta,3]$ is not an open set, nor is it a neighbourhood of $3$. However, to show that $\lim_{x \to 3}f(x)=l$ according to the more general definition of a limit, we just have to show that $3$ is an accumulation point of the domain of $f$, and that for every $\varepsilon>0$ there is a $\delta>0$ such that for all $x\in\color{red}{\operatorname{dom}(f)}$ $$ 0<|x-a|<\delta\implies |f(x)-l|<\varepsilon , . $$ – Joe Jul 15 '21 at 17:12
  • 2
    @EthanAlvaree: In other words, if $x$ is a member of the open neighbourhood $(3-\delta,3+\delta)$, and it is in the domain of $f$, then $|f(x)-l|<\varepsilon$. Does that help? – Joe Jul 15 '21 at 17:12
  • I think I got it. At $x=4$, the $\epsilon-\delta$ if-then statement would be vacuously true since $x \notin dom(f)$ for small enough $\delta$ so the $\epsilon-\delta$ implication would be automatically satisfied. But because $x=4$ is not an accumulation point, that doesn't matter and the limit wouldn't exist. However $x=3$ and $x=5$ are accumulation points and the $\epsilon-\delta$ implication is satisfied for them as well, so the double-sided limits do exist at $x=3$ and $x=5$. (Side-note: maybe I shouldn't use the word double-sided?) – EthanAlvaree Jul 15 '21 at 22:04
  • 1
    I think what helped me understand most of all was when you specified $x \in dom(f)$. When Troposphere mentioned $x \in (A \cap Z) \setminus {a}$, this was the importance of the "$\cap Z$", since $Z$ represents the domain of $f$. I think I got it now -- I wish I could accept both of your answers. Thank you both! – EthanAlvaree Jul 15 '21 at 22:08
  • 1
    @EthanAlvaree: Yes, the if-then statement is vacuously true, but as you have said, $4$ is not an accumulation point of the domain of $f$. If we defined limits at a point $a$ without requiring that $a$ be an accumulation point of the domain of $f$, then the function would approach any value near $a$ (because of the vacuously true implication). That is not a useful definition. Also, I know what you mean by two-sided limit. I agree that it's a bit weird when $f$ is not defined on one side of $a$ to use the terminology "two-sided limit", but I don't know of any better language to use. – Joe Jul 15 '21 at 22:26
  • 1
    @EthanAlvaree: Let me note one other thing that I hope does not confuse you. If $a$ is not an accumulation point of the domain of $f$, then it is called an isolated point of the domain of $f$ (the reason we use the word "isolated" should be self-explanatory). By convention, we say that $f$ is continuous at $a$, even though $a$ is not an accumulation point of the domain of $f$. So, for isolated points, the definition of $f$ being continuous at $a$ is not $\lim_{x \to a}f(x)=f(a)$. – Joe Jul 15 '21 at 22:29
  • 1
    @EthanAlvaree: This is further discussed here. – Joe Jul 15 '21 at 22:33
  • Thank you for the link - that was very helpful. One last question - I know we agreed that, using the more advanced $\epsilon-\delta$ definition, the two-sided limits $\lim_{x \to 3} f(x)$ and $\lim_{x \to 5} f(x)$ do exist. Is it also correct to say $\lim_{x \to 3^+} f(x)$ and $\lim_{x \to 5^-} f(x)$ exist? – EthanAlvaree Jul 19 '21 at 20:52
  • 1
    @EthanAlvaree: Again, this depends heavily on how you define one-sided limits. Let me offer the definition which I considered to be the most natural. The function $f:E\mapsto\Bbb{R}$ approaches the limit $l$ near $a$ from above if (i) for every $r>0$ there is an $x\in E$ satisfying $0<x-a<r$, and (ii) for every $\varepsilon>0$ there is a $\delta>0$ such that, for all $x\in E$, if $0<x-a<\delta$, then $|f(x)-l|<\varepsilon$. – Joe Jul 19 '21 at 21:17
  • Condition (i) is similar to requiring that $a$ be a limit point of $E$, except that now we are requiring that $f$ always be defined at some point above $a$, no matter how small $r$ is. According to this definition, $\lim_{x \to 3^+}f(x)$ does not exist. – Joe Jul 19 '21 at 21:17
  • Notice that while the notion of a limit can be generalised to any topological space, the notion of a one-sided limit cannot be generalised nearly as easily. For example, although $\lim_{z \to w}f(z)=l$ can easily be defined in the complex numbers, there is no such thing as $z$ approaching $w$ from above, as $z>w$ does not have a sensible definition in this context. For this reason, I believe mathematicians do not expend much effort trying to generalise the notion of a one-sided limit. This is even mentioned in @Troposphere's answer above. – Joe Jul 19 '21 at 21:17
  • @EthanAlvaree: By the way, if you have any more questions, I am happy to help. I'm glad that you are taking a deeper interest in these things. – Joe Jul 19 '21 at 21:21
  • @EthanAlvaree: Does that help? – Joe Jul 20 '21 at 19:03
  • This helps very much, thank you! It seems to me in our definition of one-sided limits, we could impose $a$ be an accumulation point of $\textrm{dom}(f) \cap [a, \infty)$ (for upper limit) or an accumulation point of $\textrm{dom}(f) \cap (-\infty, a]$ (for lower limit). Would this be equivalent to your condition (i) above? If so, this would be sufficient to exclude the upper limit from existing at places where it shouldn't (e.g. at $x=3$ and $x=4$). – EthanAlvaree Jul 20 '21 at 19:17
  • My working definition of an upper limit: Let $f$ be a function with $\textrm{dom}(f) \subseteq \mathbb{R}$. We say $\lim_{x \to a+} f(x)=L$ if and only if $a$ is an accumulation point of $\textrm{dom}(f) \cap [a, \infty)$ and for any $\epsilon > 0$, there exists $\delta > 0$ such that $0 < x-a < \delta \quad \to \quad 0 < |f(x)-L|<\epsilon$. – EthanAlvaree Jul 20 '21 at 19:19
  • @EthanAlvaree: Yes, your definition is equivalent. By the way, when writing definitions, the phrases "if" and "if and only if" mean the same thing. – Joe Jul 21 '21 at 13:32
  • @EthanAlvaree: By the way, the term "neighbourhood" is used in many different ways by different authors. In a metric space $M$ with a distance function $d$, an open neighbourhood of $p$ can refer to one of two things: (i) the set of points $x\in M$ such that $d(p,x)<r$ for some $r>0$; (ii) any open interval containing $p$. For example, $(0,10)$ is an open neighbourhood of $1$ according to definition (ii), but not definition (i). A neighbourhood of $p$ is generally defined as a set containing an open neighbourhood of $p$... – Joe Jul 21 '21 at 13:41
  • So $[0,10]$ is a neighbourhood of $1$ according to definitions (i) and (ii). However, some authors (including Rudin) require that all neighbourhoods be open. So according to Rudin's definition, a neighbourhood is the same thing as an open neighbourhood. Moreover, the term "neighbourhood" is also used in general topological spaces, but I don't know the definition works in this context. – Joe Jul 21 '21 at 13:42
  • Got it. Does that mean you suggest using the term "open set" instead of neighborhood in these definitions? – EthanAlvaree Jul 22 '21 at 04:36
  • I updated the original post with my working definitions, statement of limits relationship theorem, and its contrapositive. I am a bit concerned about the conditions of the contrapositive, which has "a is an accumulation point" as a condition. This would prevent me from using the contrapositive in many cases to say that limits don't exist, wouldn't it? For example, I wouldn't be able to use the contrapositive to prove that the limit does not exist at $x=4$. I have a feeling I might have stated the contrapositive (particularly its conditions) incorrectly. – EthanAlvaree Jul 23 '21 at 04:49
  • 1
    @EthanAlvaree: Sorry, I'll happily respond to your question tomorrow. I need to go to sleep now. – Joe Jul 24 '21 at 22:10
  • Hi @Joe, no worries, get rest, an answer from you is always worth waiting for. :) – EthanAlvaree Jul 25 '21 at 01:14
  • 1
    @EthanAlvaree: Yes, what you have written is correct. One tiny criticism: if $f$ is defined in a punctured neighbourhood of $a$, then $a$ is automatically an accumulation point of the domain of $f$, so it is redundant to require that $a$ be an accumulation point of the domain of $f$. Your statement of the theorem is essentially "if some hypotheses are met, then the following implication is true:$$\lim_{x \to a^-}f(x)=\lim_{x \to a^+}f(x)=L\iff \lim_{x \to a}f(x)=L , ."$$ – Joe Jul 25 '21 at 17:25
  • 1
    @EthanAlvaree: Now, it doesn't make sense to take the contrapositive of the entire theorem, but it does make sense to take the contrapositive of an implication within the statement of the theorem. So your theorem can equivalently be written as "if some hypotheses are met, then the following implication is true: $$ \lim_{x \to a}f(x) \neq L \iff \lim_{x \to a^-}f(x)\neq L\text{ or}\lim_{x \to a}f(x)\neq L , . $$ This is because $P\leftrightarrow Q \iff \neg Q \leftrightarrow \neg P$, and $\neg(R\text{ and S)}\iff \neg R\text{ or }\neg S$. – Joe Jul 25 '21 at 17:26
  • @EthanAlvaree: Does that answer your question? – Joe Jul 28 '21 at 12:45
  • Thanks! I just updated the theorems to remove the redundant accumulation point hypotheses. Speaking of hypotheses, should the hypotheses of both the theorem and the contrapositive be the same? Namely that $f$ is defined everywhere in a punctured neighborhood of $a$? Because this would preclude me from using the contrapositive to show that the limit does not exist at $x=4$ (since the hypothesis is not met for $x=4$). – EthanAlvaree Jul 31 '21 at 21:06
  • I think, and correct me if I'm wrong, I could use the contrapositive to show the two-sided limit does not exist at $x=3$ and $x=5$ (because those are accumulation points so the hypotheses of the contrapositive is met), but at $x=4$ I would have to say the limit does not exist only because $x=4$ is not an accumulation point. (I.e., it wouldn't be appropriate to use the contrapositive at $x=4$ because it doesn't meet the hypotheses of the contrapositive.) – EthanAlvaree Jul 31 '21 at 21:08
  • @EthanAlvaree: Yes, the hypotheses of the theorem and the contrapositive should be the same. The limit doesn't exist at $x=4$ simply because $4$ is not an accumulation point of the domain of $f$—this doesn't have anything to do with one-sided limit. The function is not defined in a punctured neighbourhood of $3$ or $5$ either, and so unless I'm mistaken I don't see how you can use the theorem connecting one-sided limits with two-sided limits. That theorem can only be applied when $f$ is defined in a punctured neighbourhood of $a$. – Joe Aug 01 '21 at 21:05
  • @EthanAlvaree: Also, the limits at $x=3$ and $x=5$ do exist, right? (At least, they do exist according to the "proper", more general, definition of a limit.) Whether you want to call these limits two-sided limits is really a terminological issue. – Joe Aug 01 '21 at 21:06
  • You're right, I meant to say they do exist at $x=3$ and $x=5$ -- that was a typo. Thanks again for your response! :) – EthanAlvaree Aug 02 '21 at 00:22
4

The theorem that you cite only applies to finite limits, not limits to infinity. Limits to infinity are an entirely different beast.

To see why, consider that if $a$ and $l$ are real numbers, $\lim_{x \to a}f(x)=l$ means "we can make $f(x)$ as close to $l$ as we like by requiring that $x$ be sufficiently close to $a$". The notation $\lim_{x \to a^+}f(x)=l$ has the same meaning, except we are only considering values of $x$ satisfying $x>a$.

On the other hand, $\lim_{x \to \infty}f(x)=l$ cannot be interpreted as "we can make $f(x)$ as close to $l$ as we like by requiring that $x$ be sufficiently close to $\infty$". It is not clear what that would even mean. Instead, the symbol "$\infty$" is being used to capture what happens to $f(x)$ when $x$ is very large, and $\lim_{x \to \infty}f(x)=l$ means "we can make $f(x)$ as close to $l$ as we like by requiring that $x$ be sufficiently large". There is no coherent definition of $\lim_{x \to \infty^+}f(x)=l$.

Joe
  • 19,636
  • Maybe not appropriate for OP's level, but "close to $\infty$" can be given a fairly coherent meaning in terms of the one-point compactification. – Charles Hudgins Jul 15 '21 at 00:00
  • 1
    @CharlesHudgins: Indeed. The problem is that in elementary calculus, the notation $x \to \infty$ just refers to what happens when $x$ becomes very large. It does not refer to a specific object "$\infty$". However, as you have mentioned, it is possible to construct new number systems where $\infty$ is a specific object. Whether it is worthwhile mentioning those systems to newcomers to calculus is something I am unsure about. – Joe Jul 15 '21 at 14:01