0

Find the area of the region bounded by $$|x| + |y| + |x+y| \leq 2$$

This question has a very nice graph.

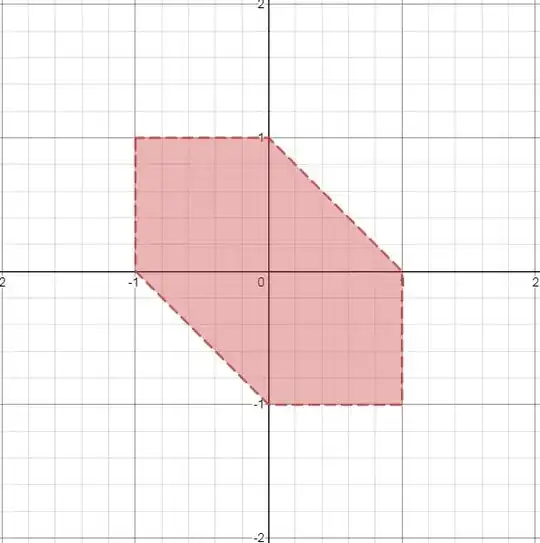
enter image description here

I know the usual steps that include checking the cases where $x<0$, $y<0$, $x\geq0$ & $y\geq0$ Quite clearly, this is a very lengthy method. Is there some solution based on symmetry or simple observation? Why can I not see two squares and two right-triangles in the equation given above?

Also, since area is involved, is there some place where integration comes into the picture?

mathx
  • 615
  • Since replacing $(x,y)$ with $(-x,-y)$ will not change the equation, so the graph has to be symmetrical about the origin. Thus you can reduce the number of cases and check only the positive $x-$axis situation. Also you can compute the area simply without involving integrals. – Anurag A Jul 14 '21 at 11:19
  • @AnuragA Thanks for that. I had tried what you mentioned. It helps a bit. But again for the $|x+y|$ term, it does not help to eliminate the casework. Also, I just want to know how integrals can be used. The solution geometrically is, obviously, much simpler always. – mathx Jul 14 '21 at 11:25

2 Answers2

3

Through the symmetry mentioned in the comments, we only need to compute the area for positive $x$, and then double the result.

The region can be split into $2$, based on $y>0$ and $y<0$.

For $y>0$, the region is given by $x+y+x+y\leq2$, which is the same as $x+y\leq1$, or $x\leq1-y$.

From $x+y\leq1$, it is obvious that $x, y\leq1$, otherwise $x+y$ would be greater than 1. The bounds for the double integration are then $[0, 1-y]$ for $x$, and $[0, 1]$ for $y$. The area of this upper region is then: $$\int_0^1\int_{0}^{1-y}1dxdy=\int_0^1(1-y-0)dy=(y-\frac{y^2}2)|_0^1=1-\frac12=\frac12$$

Now, for $y<0$ the region becomes $x-y+|x+y|\leq2$. There are 2 cases here.

If $y\geq-x$, the region is $x-y+x+y\leq2$, or $x\leq1$. Then the bounds for the double integral are $[0, 1]$ for $x$ and $[-x, 0]$ for $y$ and the area is: $$\int_0^1\int_{-x}^01dydx=\frac12$$.

And finally, if $y<-x$, the region becomes $x-y-x-y\leq2$, or $y\geq-1$. $y<-x$ means $x>-y$, therefore the bounds the double integral are $[-1, 0]$ for $y$ and $[-y, 1]$ for $x$: $$\int_{-1}^0\int_{-y}^11dxdy=\frac12$$

The area for the full $y<0$ region is therefore $\frac12+\frac12=1$, which matches geometrically.

The total area is $2(\frac12+1)=3$. This would be somewhat less lenghty if we could somehow argue that for $y<0$ the region is the $[0, 1]\times[-1, 0]$ square, but I wasn't able to do that.

Wolfuryo
  • 577
  • 5
  • 13
  • Thank you for showing how integration comes into picture. This is really not the best method. So, are you confirming that other than whatever is mentioned here and in the comments, there is no other shorter way to find the area? – mathx Jul 14 '21 at 12:03
  • I don't see any other way. – Wolfuryo Jul 14 '21 at 12:07
  • 1
    Wolfuryo That is fine. – mathx Jul 14 '21 at 12:08
2

I would suppose $ \geq 0$, the case $x < 0$ is the same. If $y \geq 0$ then the equation becomes

$$x + y + x + y \leq, 2$$

this is the same as

$$x + y \leq 1, $$

So, we have

$$x \geq 0, y \geq 0, 1 -x, \geq y$$

this is the triangle.

If $y< 0$ then we have

$$ x - y + |x + y| \leq 2$$

if we divide by 2

$$ \frac{x - y + |x+y|} {2} \leq 1$$

and this is $\max\{x, - y\} $ and we have

$$\max\{x, - y\} \leq 1$$

try to see that this is the square.

If you want to see that is the $\max$ between $x$ and $-y$ check this Show that the $\max{ \{ x,y \} }= \frac{x+y+|x-y|}{2}$.

Jonatan Garcia
  • 415