0

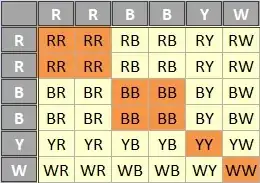
This is from Sheldon Ross's book -

Two symmetric dice have both had two of their sides painted red, two painted black, one painted yellow, and the other painted white. When this pair of dice is rolled, what is the probability that both dice land with the same color face up?

Probability aside, I want to understand how to compute the number of events that both dice land with the same color face up.

I start with total number of combinations I can get by throwing these 2 dice. Suppose for reference, the dice are marked as 1 and 2, the first dice has the faces R11, R12, B11, B12, Y1 and W1 and the second has R21, R22, B21, B22, Y2 and W2. If I am performing this experiment, I would consider the red faces showing up as one outcome, i.e., if I get any of these 4 outcomes : (R11,R21), (R11,R22), (R12,R21) and (R12,R22), I will consider as a single outcome (R,R) because the dice are symmetric.

But the textbook takes all 4 Red outcomes as different and count as 4. I want to understand why is that? To an observer, the red colored sides will look exactly same, so shouldn't it be counted as one outcome?

Please explain if I have not understood it correctly.

Ankit Seth
  • 202
  • 1
    In problems such as this it is often more convenient to "pretend" that the sides are numbered. In that way, we can get equally probable events. You can, if you prefer, speak of two similarly colored sides as being the same, but in that case you don't have equally probable events. – lulu Jul 14 '21 at 11:03
  • This comes up already with ordinary dice. If you are throwing two dice you can consider ordered or unordered outcomes. If they are ordered, then the probability throwing, e.g., $(2,2)$ is the same as throwing $(1,3)$. But if you think of unordered pairs, than ${1,3}$ is twice as likely as ${2,2}$. – lulu Jul 14 '21 at 11:05

1 Answers1

2

an easy way to understand the solution is to draw the sample space that is a table of $6\times6$ possible and equiprobable cases.

enter image description here

As you can see, the favourable cases are 10 on 36 possible. Thus the solution is $\frac{10}{36}$

tommik
  • 32,733
  • 4
  • 15
  • 34