0

There are several ways to approximate the Digamma function $\psi(x)$ that become exact for $x\to\infty$.

The simplest approximation is $$\lim_{x\to\infty}(\psi(x)-\mathrm{ln}(x))=0$$

There are other faster appromixations that involve more corrections terms (see this SE post or Digamma article in Wikipedia).

Are there approximations that become exact for $x\to1$ but deviate with growing $x$ ? The approximation shall become better for $x\to1$ for $x\ge1$ (i.e. approximations for $x<1$ are not of interest).

The aim is to approximate the Digamma function for large values $x\to\infty$ and for small values $x\ge1$. Simpler functions shall be used. Approximations that involve Zeta functions or infinite sums make the problem not simpler.

granular_bastard
  • 517
  • The Digamma-function is smooth in x=1, so why not its Taylor approximation? – nicrot000 Jun 28 '21 at 13:48
  • This would involve values from a Zeta function. The sense is to have an approximation based on simpler functions. – granular_bastard Jun 28 '21 at 15:26
  • @granularbastard Are you looking for a numerical approximation or an analytical approximation? The desire for an exact result at $x=1$ suggests the latter. – njuffa Jun 28 '21 at 23:58
  • 1
    You may use $$ \psi (x) = \log (x + 1) - \sum\limits_{n = 1}^\infty {\frac{{(\left| {G_n } \right| + 1)(n - 1)!}}{{(x + 1)(x + 2) \cdots (x + n)}}} $$ for $x\geq 1$, where $G_n$ denotes the Gregory coefficients https://en.wikipedia.org/wiki/Gregory_coefficients – Gary Jun 29 '21 at 13:55
  • @Gary This seems to be an asymptotic approximation? It is not clear to me how it fulfills the asker's requirement: "Are there approximations that become exact for $x\to1$ but deviate with growing $x$ ?". – njuffa Jun 30 '21 at 00:52
  • 2
    @njuffa This is called a factorial series. It is exact for all $x\geq 1$. – Gary Jun 30 '21 at 05:36
  • I am looking for an approximation without infinite sums. It should be in the kind of ln(x) for x→∞ (and maybe a few correction terms are possible). But I don't want an approximation that becomes exact for x→∞ but becomes exact for x→1 if approached from above. No approximation is needed for x<1. So if we go from $\infty\to1$ the approximation shall become beter. – granular_bastard Jun 30 '21 at 16:51
  • 1
    Why couldn't you just take the logarithmic derivative of the Lanczos approximation? – J. M. ain't a mathematician Jul 01 '21 at 05:08

5 Answers5

4

The Digamma function is analytic at $1$, with Taylor series

$$ \psi(z) = -\gamma - \sum_{n=1}^\infty \zeta(n+1) (1-z)^n $$

This converges for $|z-1|<1$.

EDIT: $\psi$ is analytic in $\mathbb C$ except for poles at the nonpositive integers. So $\psi(1/z)$ is analytic in the disk of radius $1$ around $1$, and its Taylor series around $1$ converges there. So if this Taylor series is $$\psi(1/z) = \sum_{n=0}^\infty c_n (z-1)^n$$, we can write $$ \psi(x) = \sum_{n=0}^\infty c_n \left(\frac{1}{x}-1\right)^n $$ and use partial sums of this as our approximations. For example, the sum up to $n=6$ is

$$-\gamma -\frac{\pi^{2} \left(\frac{1}{x}-1\right)}{6}+\left(\frac{\pi^{2}}{6}-\zeta \! \left(3\right)\right) \left(\frac{1}{x}-1\right)^{2}+\left(-\frac{\pi^{2}}{6}+2 \zeta \! \left(3\right)-\frac{\pi^{4}}{90}\right) \left(\frac{1}{x}-1\right)^{3}+\left(\frac{\pi^{2}}{6}-3 \zeta \! \left(3\right)+\frac{\pi^{4}}{30}-\zeta \! \left(5\right)\right) \left(\frac{1}{x}-1\right)^{4}+\left(-\frac{\pi^{2}}{6}+4 \zeta \! \left(3\right)-\frac{\pi^{4}}{15}+4 \zeta \! \left(5\right)-\frac{\pi^{6}}{945}\right) \left(\frac{1}{x}-1\right)^{5}+\left(\frac{\pi^{2}}{6}-5 \zeta \! \left(3\right)+\frac{\pi^{4}}{9}-10 \zeta \! \left(5\right)+\frac{\pi^{6}}{189}-\zeta \! \left(7\right)\right) \left(\frac{1}{x}-1\right)^{6} $$ where the error is about $0.0020$ at $x=2$ and $0.0206$ at $x=3$.

Robert Israel
  • 448,999
  • This is only valid for $|z-1|<1$. I am looking for an approximation that works for all values $z\ge 1$. The approximation shall be be become worse for $z\to\infty$. This is in contrast to the common formulas where the approximation becomes better if $z\to\infty$. – granular_bastard Jun 28 '21 at 14:58
  • What's your definition of "an approximation that works"? – Robert Israel Jun 29 '21 at 05:08
  • It should be good approximate for small values, but small values does not mean $|z-1|$<1. I mean small values $z\ge1$. The approximation shall become better if we approach $z\to1$ from above. The formula in the OP approximates better for $z\to\infty$ if we approach from below. Now I am just looking something opposite. – granular_bastard Jun 29 '21 at 10:00
1

The trivial $$\psi(x)=\sum _{n=0}^\infty \frac{ \psi ^{(n)}(1)}{n!}(x-1)^n \qquad \text{for}\qquad 1\leq x \lt 2$$

Another one was already given by @Robert Israel in his answer.

I suppose that there are a few other.

Edit

For illustration, I give you the solution $x_p$ of the equation $$\psi(x)-\sum _{n=0}^p \frac{ \psi ^{(n)}(1)}{n!}(x-1)^n =0.01$$

$$\left( \begin{array}{cc} p & x_p \\ 10 & 1.69006 \\ 20 & 1.82646 \\ 30 & 1.87968 \\ 40 & 1.90795 \\ 50 & 1.92547 \end{array} \right)$$

Claude Leibovici
  • 260,315
  • Of course this is the same as the other answer since the Taylor series about $1$ is unique. – Gary Jun 28 '21 at 13:59
1

Why not use the Laurent series around $0$? $$\psi^{(0)}(z)=\frac{-1}{z}+\sum_{n=0}^\infty \frac{\psi^{(n)}(1)}{n!}z^n$$

K.defaoite
  • 12,536
1

I do not know of an approximation that can make do without the use of infinite sums, but in practical terms this might be addressable by truncation or precomputation as appropriate. The following approximation that requires only elementary math is from

Peter McCullagh, "A Rapidly Convergent Series for Computing $\psi(z)$ and Its Derivatives", Mathematics of Computation, Vol. 36, No. 153, January 1981, pp. 247-248. (online)

$$\psi (1 + z) = -\gamma + \sum_{r=1}^{\infty} (-1)^{r+1} z^{r} \{c_r + r^{-r} / (z + r) \}, \qquad |z| \lt \infty,$$ where $c_r = \sum_{k=r+1}^{\infty}k^{-r-1}$. The publication provides the first fifteen $c_r$ pre-computed to twenty decimal places. I gave it a quick try in the form of an ad-hoc program and it seems to work quite well. Accuracy is best at $\psi(1)$ and diminishes as the argument increases in magnitude, as desired by the asker.

njuffa
  • 1,768
1

The following two formulas for the digamma function $\psi(z)$ both converge very rapidly as $z\to 1$, but formula (2) seems to converge slightly faster than formula (1), and also note formula (2) evaluates exactly correct at $z=1$ for all values of $K$.

$$\psi(z)=\underset{K\to\infty}{\text{lim}}\left(z \sum\limits_{k=1}^K \frac{1}{k (k+z)}-\frac{1}{z}-\gamma\right)\tag{1}$$

$$\psi(z)=\underset{K\to\infty}{\text{lim}}\left(\sum\limits_{k=1}^K\left(\frac{1}{k}-\frac{1}{k+z-1}\right)-\gamma\right)\tag{2}$$

The following figure illustrates formulas (1) and (2) for $\psi(z)$ in orange and green overlaid on the blue reference function $\psi(z)$ where both formulas are evaluated at $K=10$. As mentioned above, formula (2) illustrated in green seems to converge more rapidly than formula (1) illustrated in orange, and formula (2) also evaluates exactly correct at $x=1$ for all values of $K$.

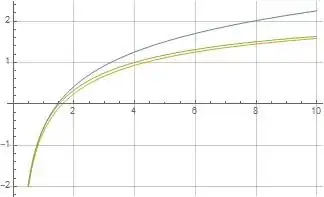
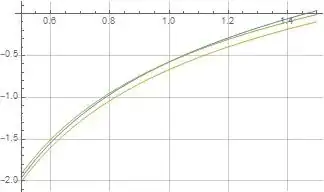
Illustration of formulas (1) and (2)enter image description here

Figure (1): Illustrations of formulas (1) and (2) for $\psi(z)$ evaluated at $K=10$ in orange and green overlaid on blue reference function

Formulas (1) and (2) above are from the Wolfram functions site.

There's also the following limit representation of the digamma function expressed in terms of the gamma function.

$$\psi(z)=\underset{s\to 0}{\text{lim}}\ \Gamma(s)\ \left(1-\frac{\Gamma (z-s)}{\Gamma (z)}\right)\tag{3}$$

For $\Re(z)>0$, the digamma function may also be expressed in terms of the Hypergeometric PFQ function.

$$\psi(z)=(z-1)\, _3F_2(1,1,2-z;2,2;1)-\gamma,\quad\Re(z)>0\tag{4}$$

Steven Clark
  • 7,363