I went through some introductory videos of this topic and this was an idea presented in each. Exactly, what does geometric algebra do different than linear algebra which makes this operation sensible?
Point is mentioned at 11:52 of this video right after introducing the geometric product of how bivectors and scalars can be added, and, again at 17:58 where a multivector with scalar, vector and bivector components is shown
This is from my book:
How can we add, e.g, a scalar and a vector? Are we not adding apples and oranges? Yes, but there is a sense in which we can add apples and oranges: put them together in a bag. The apples and oranges retain their separate identities, but there are “apples + oranges” in the bag.
The short answer is something like "because you can define anything you want in mathematics" (the video linked in the OP). And the long answer(s) depend on a choice of foundations of math that 1. was not specified in the question and 2. the vast majority of mathematicians don't have to worry about. I'll try to thread the needle, though.
Suppose, for example, that we're doing geometric algebra in two-dimensional space. Then every vector is of the form $b\mathbf i+c\mathbf j$ for scalars $b,c$; and every bivector is of the form $d(\mathbf i\wedge \mathbf j)$ for some scalar $d$. So we can consider lists of four scalars as the objects in $2\text{d}$ geometric algebra, with $\left\langle a,b,c,d\right\rangle$ being written as $a+b\mathbf i+c\mathbf j+d(\mathbf i\wedge \mathbf j)$, and any complicated expression with scalars, vectors, and bivectors able to be expanded out into the individual $\mathbf i$ and $\mathbf j$ components, so that we could identify the four scalars in the "list of four scalars" representation, if we wanted to.
In general, we can handle $n\text{d}$ geometric algebra with lists of $\binom{n}{0}+\binom{n}{1}+\cdots+\binom{n}{n-1}+\binom{n}{n}=2^n$ scalars.
A geometric algebra is a vector space where the elements are products of vectors. Suppose, for example, we are working with a 3D Euclidian orthonormal basis $ \left\{ {\mathbf{e}_1, \mathbf{e}_2, \mathbf{e}_3 } \right\} $. Then the following would all be elements of the geometric algebra that is said to be generated by this basis $$\begin{aligned} &\mathbf{e}_1 \mathbf{e}_1 \\ &\mathbf{e}_1 \\ &\mathbf{e}_1 \mathbf{e}_2 \\ &\mathbf{e}_1 \mathbf{e}_1 \mathbf{e}_1 \mathbf{e}_2 \mathbf{e}_3.\end{aligned}$$
In addition to the usual vector space axioms, a geometric algebra has a contraction axiom, defining the product of any vector with itself
$$\mathbf{x}^2 = \mathbf{x} \cdot \mathbf{x}.$$
The multivector formed by adding all of the example products above, after reduction using the contraction axiom, is $$ 1 + \mathbf{e}_1 + \mathbf{e}_1 \mathbf{e}_2 + \mathbf{e}_1 \mathbf{e}_2 \mathbf{e}_3,$$ which happens to have an element of each grade, a scalar, vector, bivector, and trivector.
I would like to present a more geometric perspective on this, based on my answer given here: https://math.stackexchange.com/a/4304117/322997
Vectors can be thought of as representing (hyper)planes. For example, in 3D space a vector can be used to represent a plane through the origin. Now, a plane $u$ can be reflected in a plane $v$ using
$$ v[u] = -vuv^{-1}, $$
where the minus sign is needed such that when you reflect $v$ in itself, the front and back of the mirror flip ($v[v] = -v$). If we now also perform a reflection in a second plane $w$, we get the rotation
$$ w[v[u]] = (wv)u v^{-1} w^{-1} = (wv) u (wv)^{-1} $$
The composition of two reflections $wv$ is called a bireflection, and could in fact be either a rotation, translation, or a boost. The picture below shows how two intersecting reflections form a rotation, while parallel reflections form a translation.
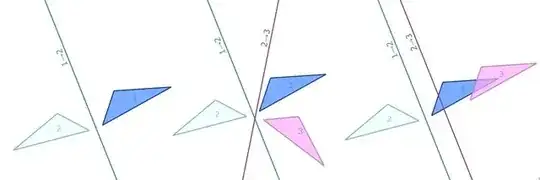
So the product of two vectors is a bireflection. The "apples and oranges" of scalar plus bivector only appear because in order to actually compute it, we would have to somehow choose a basis. Staying with the 3D example, we could choose an orthogonal basis $e_1, e_2, e_3$ such that $e_i e_j = \delta_{ij} + e_{ij}$ and represent any plane as $x = \sum_i x^i e_i$.
Now, when we compute the bireflection $wv$ we will get a scalar and bivector part: $$ w v = \sum_{ij}(w^i e_i) (v^j e_j) = \sum_i w^i v^i + \sum_{i \neq j} w^iv^j e_{ij}. $$
So just remember the truth: there are no apples and oranges. This works in any number of dimensions: the vectors of a geometric algebra $\mathbb{R}_{p,q,r}$ form the reflection group $Pin(p,q,r)$. And while it is possible to add $k$-vectors to form arbitrary multivectors, their geometric validity is debatable. When you do purely algebra, you can make any number come out of any hole. But if you make sure to follow the geometry where it leads you, you'll find there is nothing mysterious about the multivectors you end up with.
For more detail on this approach I would refer to this video, or to the Graded Symmetry Groups paper. Full disclaimer: I'm one of the authors.
