0

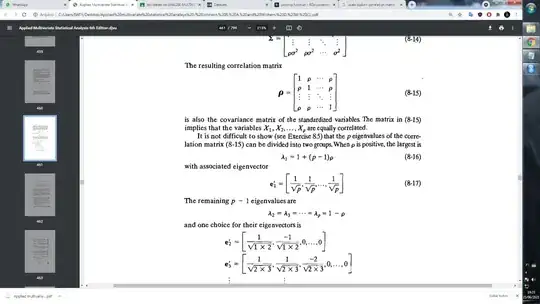
I'd like to proof that eigen values of this matrix is given by (8-16) and bellow to (8-17), my trouble is about solve p-degree polynomial. enter image description here

Davi Américo
  • 211
  • if $\rho !=1$ this matrix has rank p not 1. – Davi Américo Jun 26 '21 at 01:00
  • your question depends on knowing the matrix with all entries $1$ Call such a matrix $T.$ The eigenvectors are the same; then $\rho T$ has those eigenvalues multiplied by $\rho.$ Finally, adding $(1-\rho)I$ shifts the eigenvalues by exactly $1-\rho$ Meanwhile, see http://math.stackexchange.com/questions/1414690/matrix-with-all-1s-diagonalizable-or-not/1414925#1414925 – Will Jagy Jun 26 '21 at 01:36
  • $\mathbf{\rho_{pxp}}=\rho.\mathbf{1_{pxp}}+(1-\rho)I_{pxp}$ where $\mathbf{1}=T$. I see ones-matrix on it but i didn't get what you did after that at all, mainly the why $(1-\rho)I$ will increase each eigenvalue by $1-\rho$. I've looked through your link though. That would be more easy to see if $det(A+B)=det(A)+det(B)$ – Davi Américo Jun 26 '21 at 02:12
  • suppose we have a matrix $M$ where we know the eigenvalues. We take an eigenvector $v$ such that $Mv = \lambda v.$ Then $ (\alpha M + \beta I)v = \alpha Mv + \beta I v = \alpha \lambda v + \beta v = (\alpha \lambda + \beta) v$ – Will Jagy Jun 26 '21 at 03:32
  • Let $v$ be eigenvector to $\rho_{pxp}$. We have $\rho_{pxp}v=(\rho\mathbf{1}+(1-\rho)I_{pxp})v=\rho\mathbf{1}v+(1-\rho).v=\lambda.v$ so $\rho\mathbf{1}v=\lambda.v-(1-\rho).v$, $\mathbf{1}v=v.(\lambda-(1-\rho))/\rho$ I guess the ones-matrix has a only eigenvalue equals to $p$ so $(\lambda-(1-\rho))/\rho=p$ with that we can get $\lambda$, $\lambda-1+\rho=p\rho$ so $\lambda=p\rho+1-\rho$ finally i get $\lambda=1+(\rho-1)p$. Now what should i do to get $1-\rho$. I cannot see ones-matrix having more than eigen value different to $0$ but if you wanna stop here since you helped a lot. – Davi Américo Jun 26 '21 at 04:47
  • Ok, i see, not ignoring non-null values to eigen values of $\mathbf{1}$ we get $(\lambda-1+\rho)/p=0$ so $\lambda=1-p$ – Davi Américo Jun 26 '21 at 04:56

0 Answers0