1

While solving problems about in how many ways some numbers can be added up to another number, when they have a lower or upper bound, I've though of this problem. I'm looking for a general formula for the problem stated in the title, if such a formula exists.

I've come up with more easier versions of this problem, which I was able to solve:

Case 1. Where numbers are greater or equal to 10:

$$\ x_1+x_2+x_3=n \text{ $ $ $ $ $ $ $ $ where } 10\le x_1,x_2,x_3$$ Here, like in the case of two digit numbers, it is guaranteed that these numbers are greater or equal to $10$ but without any upper bound restrictions. So each variable is just some another variable with $10$ added, yielding the equation: $$\ x'_1+10+x'_2+10+x'_3+10=n \text{ $ $ $ $ $ $ $ $ where } 0\le x'_1,x'_2,x'_3$$ $$\text{(subtracting 30)} \Leftrightarrow x'_1+x'_2+x'_3=n-30 $$ The rest is just a simple permutation of $n-30$ ones and $2$ plus signs, yielding the result $$\binom{n-30+2}{2}, n\ge 30$$

Case 2. Where numbers are smaller than 100:

$$\ x_1+x_2+x_3=n \text{ $ $ $ $ $ $ $ $ where } 0 \le x_1,x_2,x_3 \lt 100$$ Since they are integers, the range condition can be rewritten as: $$0\le x_1,x_2,x_3 \le 99$$ Hence, for each $x_i$, there is some variable $x'_i\ge0$ that satisfies the equations $x_i+x'_i=99 \Leftrightarrow x_i=99-x'_i$. With this, the original equation can be rewritten as: $$\ 99-x'_1+99-x'_2+99-x'_3=n \text{ $ $ $ $ $ $ $ $ where } 0 \le x'_1,x'_2,x'_3 \le 99$$ This can be rearranged to the following: $$\ 99\cdot3-n=x'_1+x'_2+x'_3=297-n$$ We can now use the "stars and bars" formula we have used for the first case to arrive at the result $$\binom{n-30+2}{2}, n\le 297$$

Case 3. Where numbers are greater or equal to 10 and smaller than 100:

$$\ x_1+x_2+x_3=n \text{ $ $ $ $ $ $ $ $ where } 10 \le x_1,x_2,x_3 \le 99$$ This is the part I found myself stuck in. Applying the method from the case 1, I arrived at the equation $$\ x'_1+x'_2+x'_3=n-30 \text{ $ $ $ $ $ $ $ $ where } 0 \le x'_1,x'_2,x'_3 \le 89$$ Applying the method from the case 2, I arrived at the equation $$\ x''_1+x''_2+x''_3=267-(n-30)=297-n \text{ $ $ $ $ $ $ $ $ where } 0 \le x'_1,x'_2,x'_3 \le 89$$ This is exactly equal to the answer to the case 2, which obviously should not be. Is there something I've done false? How can the right formula be derived for this problem?

Additional information: Here is the distribution of these permutations:

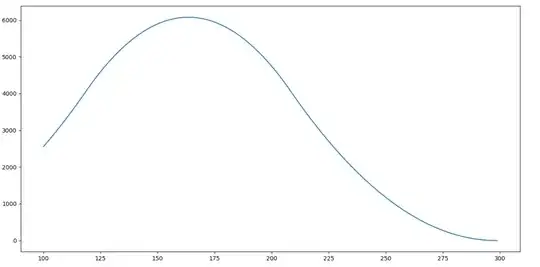
Plot of how many permutations of two digit numbers there are that add up to n

Here are the individual values and the Python script I used for creating the plot: The script

ErdemT09
  • 21
  • The technique highlighted in the answer below is called "generating functions", you can find many examples here, on MSE (here is one). – rtybase Jun 26 '21 at 07:44

1 Answers1

1

The problem is equivalent to finding the coefficient of $x^n$ in $$(x^{10}+x^{11}+x^{12}+...+x^{99})^3=(x^{10}-x^{100})^3(1-x)^{-3}$$ We know from the generalized binomial theorem that the coefficient of $x^r$ in $(1-x)^{-n}$ is $\binom {n+r-1}{r}$. Hence, since $$(x^{10}-x^{100})^3=x^{30}-3x^{120}+3x^{210}-x^{300}$$ our final answer is: $$\binom{n-28}{n-30}-3\binom{n-118}{n-120}+3\binom{n-208}{n-210}$$

This is because $n<300$ anyway, so last coefficient is ignored. Note that in case $n<100$, only first term is to be considered. If $100<n<200$, first and second terms are to be considered and of $n>200$, all three terms are to be considered for answer.

Ritam_Dasgupta
  • 5,992
  • 2
  • 8
  • 23
  • I understand how the coefficient of some number $n$ in the sequence from 10 to 99 can represent its corresponding number of ways. But I don't understand how this is equal to the multiplication on the right side of the equation. Can you please explain how these relate to each other and yield the solution?

    Your end formula is indeed correct though, it matches my computations. Thank you.

     – ErdemT09 Jun 26 '21 at 04:44
  • No it was actually incorrect. See if it's understandable now. – Ritam_Dasgupta Jun 26 '21 at 07:16