Every parabola can be represented in the general form $$\text{Axis}^2= \text{LR} \cdot (\text{Tangent})$$ where the tangent is at the vertex and LR is the latus rectum.
Update: It seems that replacing $x$ and $y$ in their standard equations with the distance from each axis gives the general equation, but I can't derive these. Can somebody help out?
Suppose point $P$ on a parabola with focus $F$ and latus rectum $4r$ has distance $p$ from the axis and distance $q$ from the vertex-tangent.
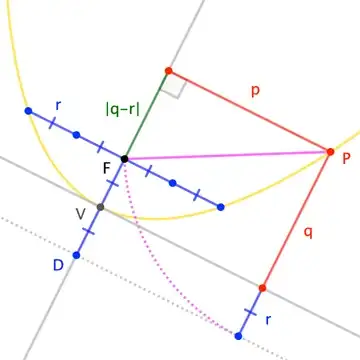
Then $\overline{PF}$ is the hypotenuse of a right triangle with legs $p$ and $|q-r|$; also, $P$ is at distance $q+r$ from the directrix. These distances are equal for a parabola, so we can equate their squares:
$$p^2+|q-r|^2 = (q+r)^2 \qquad\to\qquad p^2=4r\cdot q \tag{1}$$
Now, we simply observe that the (signed) distance from a point $(x,y)$ to a line with equation $ax+by+c=0$ is given by the normalized form of the equations left-hand side; ie, $$\text{distance to line} = \frac{ax+by+c}{\sqrt{a^2+b^2}} \tag{2}$$ so we can write $(1)$ as $$(\text{normalized eqn of axis})^2 = (\text{length of latus rectum})\cdot(\text{normalized eqn of vertex-tangent}) \tag{1'}$$ as desired. $\square$
Importantly, the equation of a line has a sign ambiguity (eg, $1x+2y-3=0$ represents the same line as $-1x-2y+3=0$). In the context of $(1')$, the ambiguity with the axis equation is rendered irrelevant because of squaring; however, the ambiguity with the vertex-tangent equation corresponds to the parabola opens. That is to say: a given parabola requires an unambiguous vertex-tangent equation; namely, $Ax+By+C=0$ where normal vector $(A,B)$ points in the direction that the parabola opens.
To generalize to other conics, recall that a point on a conic eccentricity $e$ satisfies $$(\text{dist to focus})=\text{eccentricity}\cdot(\text{dist to directrix})\tag{3}$$ It is "known" that, for a central conic with major/transverse radius $a$, the center-to-focus distance is $c=ae$, and the center-to-directrix distances is $d:=a/e$; therefore, we can calculate the vertex-to-focus and vertex-to-directrix distances as $$|VF|=\sigma(a-c)=\sigma a(1-e) \qquad\qquad |VD|=\sigma(d-a)=\sigma\frac{a}{e}(1-e) \tag4$$ where $\sigma$ is $+1$ for ellipses and $-1$ for hyperbolas. With these, the square of relation $(3)$ gives this analogue of $(1)$: $$p^2+|q-|VF||^2 = e^2(p+|VD|)^2 \quad\to\quad p^2 + q^2(1-e^2)=2\sigma a (1-e^2) \cdot q \tag5$$ Now, note that if the minor/conjugate radius of the conic is $b$, then $b^2=\sigma(a^2-c^2)=\sigma a^2(1-e^2)$, so that we can write $(5)$ as $$p^2 + q^2(1-e^2)=\frac{2b^2}{a}\cdot q \tag6$$ But $2b^2/a$ is precisely the length of the latus rectum, so this gives us the analogue of $(1')$:
$$(\text{axis eqn})^2+(\text{tangent eqn})^2(1-\text{eccentricity}^2)=(\text{latus rectum})(\text{tangent eqn}) \tag{7}$$
where the equations are normalized, as before. $\square$
You want the form $$\frac{(ay-bx-af_2+bf_1)^2}{a^2+b^2}-(2\frac{bf_2+af_1+c}{\sqrt{a^2+b^2}})\frac{(ax+by-\frac{bf_2+af_1-c}{2})}{\sqrt{a^2+b^2}}=0$$ which can be proved is the same by expanding both forms and comparing.
– Jan-Magnus Økland Aug 03 '21 at 07:58