Give an example of a function $f : R → R$ whose graph is invariant under a $90^{\circ}$ rotation about the origin.

Question

Give an example of a function $f : R → R$ whose graph is invariant under a $90^{\circ}$ rotation about the origin.

The answer to this question was the function $$ f(x) = \frac{x}{|x|} - (-1)^{\lfloor{-|x|}\rfloor}x. $$

There was no explanation given. How does one come up with such a complicated function? The link given below also has some interesting examples, however, I want to know if some standard technique exists for solving such questions.

Will the answer be correct if the floor function is replaced by the ceiling function?

Finally, is there any place that you think/know such a graph may show up?

Answer 1

Let $f$ be such a function. Then necessarily $f(0)=0$. For every $x\ne 0$, $f$ maps cyclically $x\mapsto f(x)\mapsto -x \mapsto -f(x)\mapsto x$, and the four numbers $x,f(x),-x,-f(x)$ must be distinct. In fact, exactly two of them are positive. Let $$A=\{\,x\in \Bbb R\mid x>0\land f(x)>0\,\}$$ and $$ B=\{\,x\mid x>0\land f(x)<0\,\}.$$ Then $\Bbb R_{>0}$ is the disjoint union of $A$ and $B$, and we see that $f$ maps points in $A$ to points in $B$, these to points in $-A$, these to points in $-B$, and these back to $A$. Upon closer look, $f$ induces a bijection $A\to B$.

---

This suggest the following method to describe the most general function of the desired kind:

Pick a continuum-sized subset $A\subset \Bbb R_{>0}$ such that $B:=\Bbb R_{>0}\setminus A$ is also continuum-sized. Pick a bijection $g\colon A\to B$ and define $$ f(x)=\begin{cases}0&x=0\\ g(x)&x\in A\\ -g^{-1}(x)&x\in B\\ -g(-x)&-x\in A\\ g^{-1}(-x)&-x\in B \end{cases}$$

Indeed, one "readily" verifies that the graph of such $f$ has the desired rotational symmetry.

Answer 2

Let $\mathrm{P}(a,f(a))$ be a point on the graph of $f$. If you rotate that point $90$ degrees anticlockwise about the origin, then $\mathrm{P}$ is mapped to $\mathrm{P'}(-f(a),a)$ (there are a number of ways you can justify this, e.g. with matrices). If the graph of $f$ is invariant under a $90$ degree rotation, then it must be the case that $\mathrm{P'}$ also lies on the graph of $f$. Symbolically, $$ f(-f(a))=a \, .\tag{*}\label{*} $$ So the functions that are invariant under a $90$ degree rotation are precisely those that are solutions to $\eqref{*}$. I believe it is difficult, if not impossible, to find the general solution of this equation, so naturally we look for examples.

To make the problem easier for ourselves, suppose that $f$ is even or odd. If $f$ is even, then $$ f(-f(a))=f(f(a))=a \implies f(a)=f^{-1}(a)\, . $$ This means that any even function which is its own inverse satisfies $\eqref{*}$. Unfortunately, it is impossible for an even function to be its own inverse! Try figuring out why.

If $f$ is odd, then the equation boils down to $f(f(a))=-a$. This equation has been asked about on MSE before. Alex Jordan's answer mentions the function $g(x)=\frac{x}{|x|}-(-1)^{\lceil|x|\rceil}x$ which looks almost identical to the function you asked about in your question (the only difference is the behaviour of the function at the endpoints of each line segment):

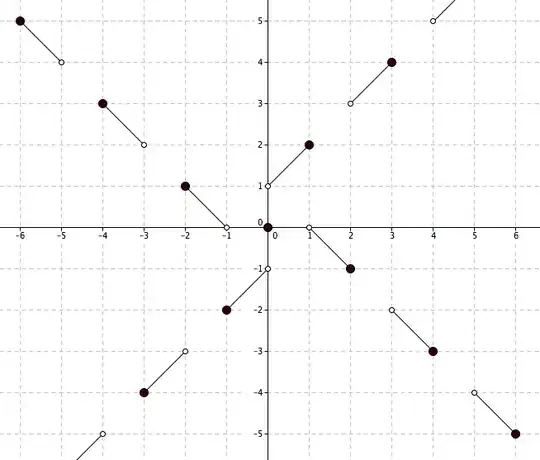
This visual tells us something important. While the formulae describing the functions $f$ and $g$ look formidable, the graphs of the functions themselves are fairly simple-looking. It's easy to see that the above graph describes a function which satisfies your equation—the hard part is finding a concise formula that describes the function. Almost certainly the person who conceived of this example thought of the graph first, and only then found a clever way of describing the function using a formula.