I have two functions $f$ and $g$ defined as:
$c:=x^3+x^2+x$
$d:=20\sin x^2-5$
I am trying to find the intersections of these using Maple $16$. How would I do this?
I have two functions $f$ and $g$ defined as:
$c:=x^3+x^2+x$
$d:=20\sin x^2-5$
I am trying to find the intersections of these using Maple $16$. How would I do this?
Here is the command
fsolve( x^3+x^2-x=20*sin(x^2)-5, x=0..2 );
If you give maple the above command you will get the answer
$$ 0.4960649664. $$
Still there are other points of intersection and its your job to find them.
I think you can use this command :
f := x^3+x^2+x = 0;
g := 20*sin*x^2-5 = 0;
fsolve({f, g});
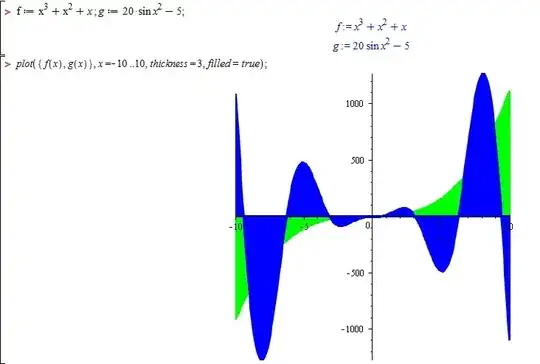
The two expressions c and d intersect at the values of x for which their difference is zero. So you can compute the roots of c-d, or plot that.
For this example it happens that all the roots fall within the default ranges of the two commands (Roots and plot) used below. For other examples you might supply additional arguments to specify the range.
c := x^3+x^2-x:
d := 20*sin(x^2)-5:
Student:-Calculus1:-Roots(c-d, numeric);
[-3.372171392, -3.196493666, -2.489209992, -1.704885557,
-0.5361086923, 0.4960649664, 1.614439567]
plot(c-d);

I have two functions f and g defined as:
f:=x^3+x^2-x g:=20sinx^2-5
Now it could be fine.
– Lukas Jun 11 '13 at 21:28