"Deriving" the epsilon-delta definition

Question

The intuitive definition normally says that

The limit of $f(x)$ as $x \to c$ is $L$ iff $f(x)$ approaches $L$ as $x$ approaches $c$.

The obvious problem with this is that the words ''tends'', ''approach'' and ''near'' are not exact.

Look at the table showing an estimation method for finding the limit of $f(x)=x^2$ as $x \to 2$ (excel rounded some stuff)

It seems like $x^2$ is approaching 4. However, why shouldn't we say it is approaching 4.0000001.

If we tested values of $x$ between $2$ and $\sqrt{4.0000001}$, we would see that $f(x)<4.0000001$. Therefore $f(x)$ cannot be approaching it.

As a result I said that:

The limit of $f(x)$ as $x\to c$ is not $D$, if $x$ can be made to sit in an interval containing $c$, such that the image of that interval through $f$ does not include $D$

I just noticed that this is a flawed conclusion. Since $x \neq c$ ($x\to c$ means that $x$ cannot be at $c$), that means the image of an interval containing $c$ would not include $f(c)$, which for continuous functions is the limit

Based on this I thought a more formal way of defining a limit is:

If the limit of $f(x)$ as $x\to c$ is $L$, then $f(x)$ always sits in an interval containing $L$, no matter how close $x$ is to $c$

Lassadar has shown that this definition is false since ''an interval'' could be $(-\infty, \infty)$ which includes all $L\in \mathbb{R}$ and $f(x)$ so, by my definition, every number would pass as the limit

I just took the opposite of my earlier conclusion.

However, I am having trouble going from my definition to the true epsilon-delta definition of a limit.

Edit: How would you create a formal definition from the intuitive one like I've tried to do here?

Answer 1

In Michael Spivak's Calculus, he gives a brilliant piece of exposition (pages 97-98) that guides the reader in how to turn the intuitive idea of a limit into a mathematically rigorous one. I will leave the exact quote here:

The time has now come to point out that of the many demonstrations about limits which we have given, not one has been a real proof. The fault lies not with our reasoning but with our definition. If our provisional definition of a function was open to criticism, our provisional definition of approaching a limit is even more vulnerable. This definition is not sufficiently precise to be used in proofs. It is hardly clear how one "makes" $f(x)$ close to $l$ (whatever "close" means) by "requiring" $x$ to be sufficiently closer to $a$ (however close "sufficiently" close is supposed to be). Despite the criticisms of our definition you may feel (I certainly hope you do) that our arguments were nevertheless quite convincing. In order to present any sort of argument at all, we have been practically forced to invent the real definition. It is possible to arrive at this definition in several steps, each one clarifying some obscure phrase which still remains. Let us begin, once again, with the provisional definition:

The function $f$ approaches the limit $l$ near $a$, if we can make $f(x)$ as close to $l$ as we like to $l$ by requiring that $x$ be sufficiently close to, but unequal to, $a$.

The very first change which we made in this definition was to note that making $f(x)$ close to $l$ meant making $|f(x)-l|$ small, and similarly for $x$ and $a$:

The function $f$ approaches the limit $l$ near $a$, if we can make $|f(x)-l|$ as small as we like by requiring that $|x-a|$ be sufficiently small, and $x\neq a$.

The second, more crucial, change change was to note that making $|f(x)-l|$ "as small as we like" means making $|f(x)-l|<\varepsilon$ for any $\varepsilon>0$ that happens to be given to us:

The function $f$ approaches the limit $l$ near $a$, if for every number $\varepsilon>0$ we can make $|f(x)-l|<\varepsilon$ by requiring that $|x-a|$ be sufficiently small, and $x\neq a$.

There is a common pattern to all of the demonstrations about limits which we have given. For each number $\varepsilon>0$ we found some other positive number, $\delta$ say, with the property that if $x\neq a$ and $|x-a|<\delta$, then $|f(x)-l|<\varepsilon$. For the function $f(x)=x\sin1/x$ (with $a=0$, $l=0$), the number $\delta$ was just the number $\varepsilon$; for $f(x)=\sqrt{|x|}\sin1/x$ it was $\varepsilon^2$; for $f(x)=x^2$ it was the minimum of $1$ and $\varepsilon/(2|a|+1)$. In general, it may not be at all clear how to find the number $\delta$, given $\varepsilon$, but it is the condition $|x-a|<\delta$ which expresses how small "sufficiently" small must be:

The function $f$ approaches the limit $l$ near $a$, if for every $\varepsilon>0$ there is some $\delta>0$ such that, for all $x$, if $|x-a|<\delta$ and $x\neq a$, then $|f(x)-l|<\varepsilon$.

This is practically the definition that we will adopt. We will make one trivial change, noting that "$|x-a|<\delta$ and $x\neq a$" can just as well be expressed $0<|x-a|<\delta$".

DEFINITION: The function $\pmb{f}$ approaches the limit $\pmb{l}$ near $\pmb{a}$ means: for every $\varepsilon>0$ there is some $\delta>0$ such that, for all $x$, if $0<|x-a|<\delta$, then $|f(x)-l|<\varepsilon$.

Answer 2

Informally, $L$ is the limit if $f(x)$ remains close to $L$.

"Close" is not difficult, it actually means arbitrarily close, i.e. $|f(x)-L|<\epsilon$ for an arbitrary $\epsilon$.

The key point is "remains", which we interpret as "$f(x)$ is close for all $x$ in some neighborhood of $c$".

We don't want to specify this "some", to allow maximum freedom in the proofs. All that matters is that such a neighborhood exists. Now we have all ingredients: for any $\epsilon$, we can find a neighborhood of $c$ where $f(x)$ remains close to $L$:

$$\forall \epsilon>0:\exists \delta>0:|x-c|<\delta\implies|f(x)-L|<\epsilon.$$

---

We omitted two little technicalities:

• we don't want to take into account $f(c)$, so that a limit is defined even for a function that is discontinuous or undefined at $c$;

• we can only care about the values of $x$ in the domain of $f$, so undefined values of $f$ in the neighborhood of $x$ do not matter.

$$\forall \epsilon>0:\exists \delta>0:\color{green}{ 0<}|x-c|<\delta\color{green}{\land x\in\text{dom}(f)}\implies|f(x)-L|<\epsilon.$$

Answer 3

I improved heropup's tremendous answer, which is user-friendlier and mellower than Spivak's exposition.

---

Imagine the following Socratic dialogue.

Teacher: What does $\lim\limits_{x\to a} f(x) = L$ mean?

Student: It means that the limit of the function $f(x)$, as $x$ approaches $a$, equals $L$.

Teacher: Yes, but what does that actually MEAN? What are we saying about the behavior of $f$?

Student: [Pauses to think.] I guess what we are saying is that for values of $x$ "close to" $a$, the function $f(x)$ becomes "close to" $L$.

Teacher: OK. So how are you defining the concept of "close to?" In particular, how does math quantify the notion of "closeness"? Does "close to" mean $x = a$?

Student: No — well — maybe sometimes! Of course, if $f(a)$ is well-defined, then we just have $f(a) = L$ — but this is plain vanilla, and trivial. The whole point of limits is to describe the function's behavior around the point $x = a$, even when $f$ ISN'T defined at $a$.

Teacher: Right, but you didn't answer my question. So how would you mathematically define "closeness"?

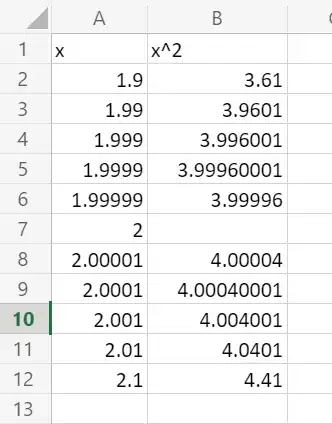
Student: [Long pause.] I'm not sure. Well, hold on. Let me try a geometric argument. When a number $x$ is "close to" another number $a$, we are really talking about the distance between these numbers being small. Like $2.00001$ is "close to" $2$, because the difference is $0.00001$.

Teacher: But that difference — which you call "distance" — isn't necessarily "small" in and of itself, is it? After all, isn't $10^{-10^{100}}$ much smaller than $10^{-5}$? "Small" is relative.

Student: [With irritation] Yeah, but you know what I mean! If the difference is small enough, then the limit exists!

Teacher: [Chuckles] Yes, I see what you're getting at! But so far, all you've been doing is choosing different vocabulary to describe the same concept. What is "distance"? What is "small enough?" We are mathematicians — how can improve this inaccurate and imprecise words? Take your time to think about this.

Student: [Sighs] What I was doing before, I was calculating a difference between $x$ and $a$, and calling it "small" if it looked like a small number. But what matters ISN'T the signed difference, but the absolute difference $|x - a|$. Since (as you put it) "small is relative," let's instead use a variable, say $δ$ (to abbreviate "difference"), to represent some bound... [trails off]

Teacher: Go on...

Student: All right. So if $|x-a| < δ$, then $x$ is "close to" $a$. We choose some number $δ$, in some way that quantifies the extent of closeness.

Teacher: OK. Is $δ$ allowed to be zero?

Student: Oh, of course not, no! I forgot. No, we need $\color{red}{0 < |x - a| < δ}$. Then $x$ is "delta-close" to $a$, or in a "delta-neighborhood" of $a$.

Teacher: All right. Now how are you going to tie $δ$ to the behavior of $f$?

Student: [Exasperated] Yes, yes, I'm getting to that part. As I said, the limit is something where if $x$ is "close to" to $a$, then $f(x)$ is "close to" $L$. Obviously, $f(x)$ can have a different extent of "closeness" to $L$, as $x$ does to $a$.

For example, if $f(x) = 2x$, then when $x$ is within $δ$ units of (for example) $1$, then $f(x)$ is only bounded within $2δ$ units of $2$, since $0 < |x-1| < δ$ implies that $0 < |2x - 2| = |f(x) - 2| < 2δ$. But functions can be arbitrarily (although not infinitely) steep. How can we quantify the relationship between the closeness of $x$ to $a$, as this closeness impacts the closeness of $f(x)$ to $L$?

Teacher: You actually touched on it, when you said that functions can be arbitrarily but not infinitely steep. Stated informally another way, it means that the function's value can change very rapidly — in fact, as rapidly as you please — but only finitely so, for some fixed change in $x$. So if you wanted to guarantee shrinking the difference between $f(x)$ and $L$ as small as you please, while not necessarily zero, how would you do it?

Student: [Long pause.] I need help.

Teacher: So far, you've been thinking about using (as you put it) "delta-closeness" to force $f(x)$ to be "close to" $L$. But what if you turned it around and instead said, I'll force $f(x)$ to be as close as I please to $L$? Then what does this closeness of $f(x)$ say about how close $x$ is to $a$? That way, you are guaranteeing that $f(x)$ becomes close to $L$, but the cost of that guarantee is that we need to guarantee that...

Student: [Interrupts] Oh, oh! I get it now! Yes. What we need to say is that for a given amount of "closeness" of $f(x)$ to $L$, a $δ$-neighborhood around $a$ where (if you pick any $x$ in that neighborhood) will guarantee $f(x)$ to be "close enough" to $L$ — that $f(x)$ will be within that given amount of closeness. In other words, we pick some "tolerance" or error bound between $f(x)$ and the limit $L$ that is our criterion for "close enough." And for that closeness, some set of corresponding $x$-values close to $a$ will guarantee that $f(x)$ meets the closeness criterion.

Teacher: Good, good. But how do we formalize this?

Student: Well, we need another variable to describe the extent of closeness between $f(x)$ and $L$...let's use $ε$, to abbreviate "error." As we did before, we use the absolute difference $|f(x) - L|$ to describe the "distance" between $f(x)$ and $L$. So our criterion has to be $\color{lightseagreen}{|f(x) - L| < ε}$. This time, we get to pick $ε$ freely, because it represents how much error we will tolerate between the function's value and its limit. We must be able to choose this tolerance to be arbitrarily small, but not zero.

Teacher: [Looks on silently, smiling]

Student: So let's define a procedure. Pick some $ε > 0$. Then whenever $\color{red}{0 < |x - a| < δ}$ (in other words, for every $x$ in a $\delta$-neighborhood of $a$), then $\color{lightseagreen}{|f(x) - L| < ε}$.

But I feel like something is missing, because there might not be such a $δ$. For example, if $$f(x) = \begin{cases}-1, & x < 0 \\ 1, & x > 0 \end{cases}$$, then if I pick $ε = 1/2$, the "jump" in $f$ at $x = 0$ has size $2$. So no matter how small I make the $δ$-neighborhood around $a = 0$, this neighborhood will always contain $x$-values that are negative, as well as $x$-values that are positive, which means any such $\delta$-neighborhood will have points where the function has values $1$ and $-1$. It would be impossible to pick a limit $L$ that is simultaneously within $1/2$ unit of $1$ and $-1$, let alone simultaneously arbitrarily close to $1$ and $-1$.

Teacher: Correct. Good job on finding a function that lacks such a $δ$. But why does this function lack such a $δ$?

Student: I don't get what you mean.

Teacher: Remember how we were talking about guaranteeing the (absolute) difference between $f(x)$ and $L$ to be shrunk as small as you please? What consequence does this guarantee have on the $δ$-neighborhood?

Student: Well, there has to be some relationship. As our error tolerance decreases, fewer $x$-values around $a$ will satisfy that tolerance, right? So $δ$ must depend in some way on our choice of $ε$. Well, except in trivial cases like if $f(x)$ is a constant, then any $δ$ works. But the point is the EXISTENCE of a $δ$. It doesn't have to be the largest, or even unique. We merely have to be able to find a sufficiently "small" neighborhood, for which all $x$-values in that neighborhood around $a$ will have function values $f(x)$, within the error tolerance we specified to $L$.

Teacher: Right. So if you were to put all of this together, how would you define the concept of a limit?

Student: I'd say that $$\lim_{x \to a} f(x) = L$$ if, for any $\epsilon > 0$, there exists some $δ > 0$ such that for every $x$ satisfying $\color{red}{0 < |x - a| < δ}$, one also has $\color{lightseagreen}{|f(x) - L| < ε}$.