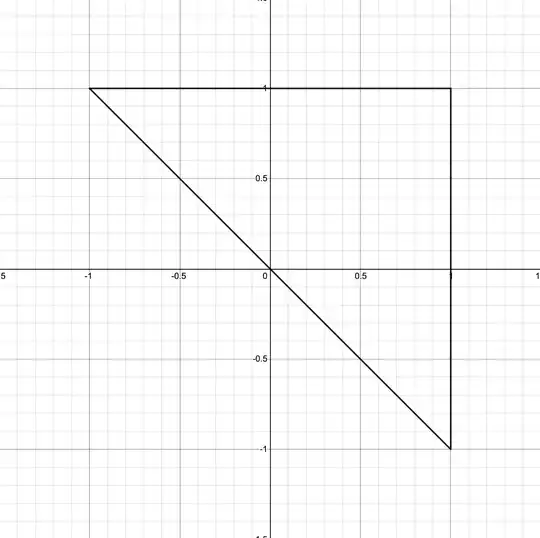
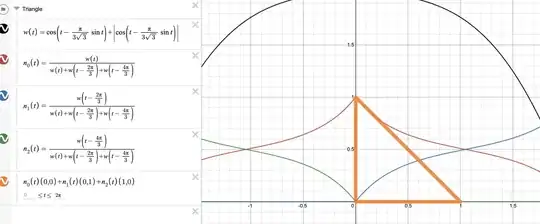
I've been trying to find a parametric equation for a triangle because I was inspired by J.M. isn't a mathematician's answer where they provided this parametric equation for a rectangle:
$x=p(|\cos t|\cos t+ |\sin t|\sin t)$
$y=q(|\cos t|\cos t- |\sin t|\sin t)$
For the right triangle, I think we can still use parts of this equation. For example, $|\cos t|\cos t+ |\sin t|\sin t$ remains constant in quadrants 1 and 3. So here, we'd need a function constant in 1 and 2, one for 2 and 3, and then 1 diagonal side with 2 changing functions.
I think we can use $\cos^2 t+|\sin t|\sin t$ as the equation constant in quadrants 1 and 2. And then from there, I think we can put that as the y and the other one as the x like so:
$x=|\cos t|\cos t- |\sin t|\sin t$
$y=\cos^2 t+|\sin t|\sin t$
Where does one go next? How can we do this with an equation for a triangle building off of the parametric equation for a rectangle that we already have? Thanks!