3

I'll state my question up-front, and then provide some motivation afterwards. Is there an example of a function that is

  • Defined in a neighbourhood of a point $a$,
  • Continuous at $a$,
  • But neither the left-hand nor the right-hand derivative exists at $a$,

and that it is 'visually obvious' that the function has these properties (so pathological functions like the Weierstrass function are excluded). For the purposes of this question, I will define 'visually obvious' as meaning that it is possible to guess that the function has the above properties just by looking at its graph.

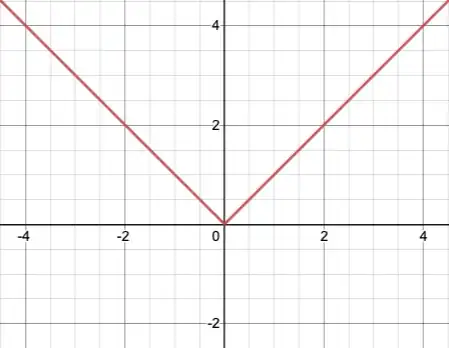
The function $f(x)=|x|$ is probably the simplest example of how a function can be continuous, and yet not differentiable, at a point:

Graph of |x|

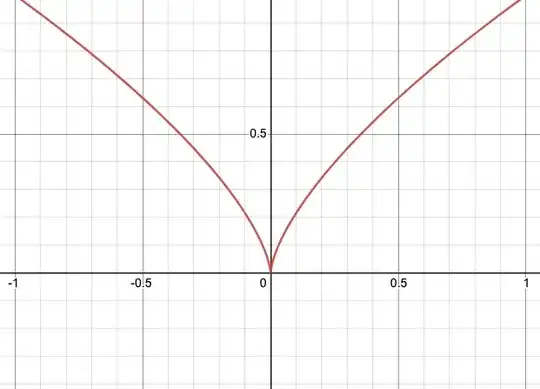
It is clear just by looking at the graph that $f$ is continuous at $0$, but $f'(0)$ does not exist as $f'_+(0)=1$ and $f'_-(0)=-1$. However, what I find unsatisfying about this example is that $f$ is still fairly well-behaved around $0$—it is meaningful to ask about the 'rate of change' of the function, it's just that we get different answers when we zone in from the left-hand side compared to the right-hand side. I'm looking for a function where it is not meaningful to talk about the 'rate of change' at all, and yet the function is still continuous at the point in the question.

Joe
  • 19,636
  • 2
    What is semi-differentiability? I can't find an exact definition for it – tryst with freedom Jun 14 '21 at 16:18
  • So are we need to find out a function which is continuous at a point but one sided derivative not exist at the same point . Is it the summary of whole problem ? –  Jun 14 '21 at 16:28
  • The question is not clear to me what about $xsin(1/x)$ suitabley defined at $0$ ? – Vivaan Daga Jun 14 '21 at 16:30
  • Something like this? – Klaus Jun 14 '21 at 16:33
  • 2
    @Buraian: A function is semi-differentiable at a point if the left-hand derivative exists or the right-hand derivative exists. So $|x|$ is semi-differentiable at $0$, for example; $x^2$ is also semi-differentiable at $0$ (because it is differentiable at $0$). However, the function$$ f(x)=\begin{cases} x\sin(1/x) &\text{if $x\neq0$} \ 0 &\text{if $x=0$} \end{cases} $$ is not semi-differentiable at $0$. – Joe Jun 14 '21 at 16:45
  • 1
    @AmitMittal: Yep, neither of the one-sided derivatives are allowed to exist. Sorry if that was not clear. – Joe Jun 14 '21 at 16:45
  • @PaxDaga: What exactly isn't clear to you? I am happy to explain. Anyway, $x\sin(1/x)$ is a good example—you can post that as answer, if you wish. – Joe Jun 14 '21 at 16:46
  • @Klaus: That's an interesting example. Perhaps it is not 'visually obvious', but this is a subjective term anyway. – Joe Jun 14 '21 at 16:48
  • I don’t see why you are looking at functions that are continuous on a neighbourhood for your examples. Any function that is only continuous at a and not anywhere else provides a fine example like say the...what’s it called, thomae function? Popcorn? Don’t remember... – Calvin Khor Jun 14 '21 at 17:02
  • @CalvinKhor: Not continuous in a neighbourhood of $a$, but defined in a neighbourhood of $a$. The reason I specified this is that functions such as $f(n)=n$ for integer $n$ are trivially continuous at each point, but not differentiable. However, we couldn't even conceivably find the derivative of $f$, as the concept of "differentiability at the point $a$" only applies to functions which are defined in a neighbourhood of $a$. – Joe Jun 14 '21 at 17:06
  • 2
    @Buraian: Apparently the term semi-differentiable has been raised to "semi-standard terminology" by Wikipedia writers who don't have much of a background in these matters (evidenced to me by the inappropriate and scant reference list there). Note, for example, the term is used here (middle p. 770) for a semicontinuity analog of differentiability. The many decades-old standard terms are "unilateral derivative" and "one-sided derivative". – Dave L. Renfro Jun 14 '21 at 17:35
  • @DaveL.Renfro: I've edited my post to use more standard terminology. – Joe Jun 14 '21 at 17:39
  • 1
    For what it's worth, my comment wasn't intended as a criticism your usage, as I assume the term "semi-derivative" is being spread by the Wikipedia page, which has only three references --- one a lesser known calculus text, one a research paper having virtually no reference significance for the topic at hand, and Dirac's quantum mechanics book (?!?). While I'm here, you might find Klymchuk's Counterexamples in Calculus useful. – Dave L. Renfro Jun 14 '21 at 17:54
  • @DaveL.Renfro: That's a very nice suggestion. Thank you. Instructional counterexamples are of immense value to me: I recently learnt about Volterra's function, which is differentiable everywhere, but the derivative is bounded everywhere, and nowhere Riemann integrable. These examples always help me refine my intuition. – Joe Jun 14 '21 at 17:58
  • In a certain sense, almost all functions with a bounded derivative are not Riemann integrable on any non-singleton interval, and even worse than this. Not being Riemann integrable on an interval is equivalent to the derivative being discontinuous on a set of positive measure, which allows for "sortta nice" functions that are also continuous on a set of positive measure (which Volterra functions are). However, "most" functions having a bounded derivative are such that the derivative is continuous only a set of measure zero (and worse still). – Dave L. Renfro Jun 14 '21 at 18:05

3 Answers3

8

Consider the function $x\sin(1/x)$, continuously extended at $0$. The left and right derivatives at $0$ don't exist as $\sin(1/h)$ keeps oscillating between $-1$ and $1$ as $h\to 0$:

Graph of xsin(1/x)

Joe
  • 19,636
Vivaan Daga
  • 5,531
3

You don’t seem to have understood my comment so let me try an answer. The weierstrass function, $|x|^s$, $x\sin1/x$, these functions are all continuous on a neighbourhood of 0. But your question is asking for functions continuous only at one point. So you can consider the function $f:\mathbb R\to\mathbb R$,

$$f(x)=\begin{cases} x &x\in \mathbb Q\\ -x &x\not\in \Bbb Q\end{cases}$$ Note that the function is everywhere defined on $\mathbb R$. Its graph is X shaped, consisting of the two lines $y=\pm x$ (what you can’t ‘draw’ is that there are infinitely many holes in any interval.) Clearly there are two candidates for the (left or right) gradient at $0$; since the (left or right) gradient must be unique, it’s not (left or right) differentiable at $0$. But it is continuous at $0$. It’s not continuous anywhere else (and therefore, not differentiable anywhere else.)

Calvin Khor
  • 34,903
2

Another fairly standard example is $f(x) = x^{2/3}$, which (like the absolute value function) has a cusp at $x = 0$, but which (unlike the absolute value function) has neither a left-handed nor a right-handed derivative, because the graph of $y=f'(x)$ has a vertical asymptote at $x = 0$. enter image description here

mweiss
  • 23,647
  • My favourite version of this is $|x|^{s-1}x$ whose graph is a differentiable curve but the graph coordinates break down in the manner you described – Calvin Khor Jun 15 '21 at 00:41