The following hopefully explains the "split integral into two" statement you mentioned.
If you take two exponentials $X$ and $Y$ with support $\mathbb{R}^+_0$ then the variable $Z=X-Y$ has support $\mathbb{R}$.
To arrive at the "convolution" of the two, just find the values of $X$ and $Y$ so that their difference is $Z$. A graph is useful for explaining this:
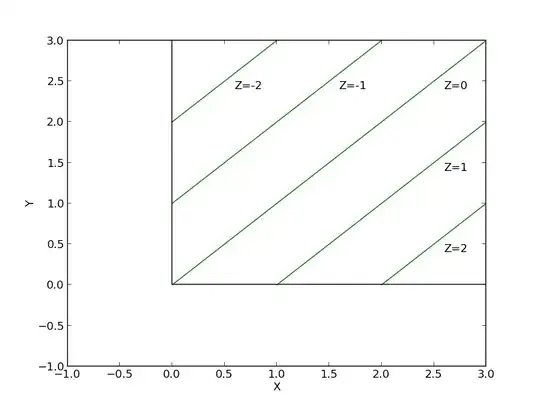
Basically, the "convolution" needs to integrate along the green lines.
With this you can see why it is good to split it into two parts: the minimum $X$ or $Y$ is not smooth at $Z=0$.
So, if $z\geq0$ we need to consider values of $x \geq z$ and $y \geq 0$, which means we do the integral:
$$p_+(z) = \int_0^\infty p_X(s+z)p_Y(s) ds$$
$$ = \int_0^\infty f(s+z)g(s) ds$$
$$ = \lambda\mu\int_0^\infty e^{-\lambda (s + z) - \mu s }$$
$$ = \lambda\mu e^{-\lambda z}\int_0^\infty e^{-(\lambda + \mu)s}$$
$$ = \frac{\lambda\mu}{\lambda+\mu}e^{-\lambda z}$$
and for $z \leq 0$ we consider the values of $x \geq 0$ and $y \geq -z$, which means we do the integral:
$$p_-(z) = \int_0^\infty p_X(s)p_Y(s-z) ds$$
$$=\frac{\lambda\mu}{\lambda+\mu}e^{\mu z}$$
Combining the two gives:
$$p(z) = \frac{\lambda\mu}{\lambda+\mu} \left\{\begin{array}{ll}
e^{-\lambda z} & z \geq 0 \\
e^{\mu z} & z \leq 0
\end{array}\right.$$
Although I agree with Did that indicator functions are a way forward, but they have the consequence of changing the support and introducing a measure zero regions. They are not necessary if you keep the support of the random variables in mind.
Regarding Did's question:
First, the general problem with using indicators...
There are two definitions of an exponential distribution we can work with, one can be written $A = \left(\mathbb{R}^+, \mathcal{B}(\mathbb{R^+}), \mu\right)$ and the other $B = \left(\mathbb{R}, \mathcal{B}(\mathbb{R}), \nu \right)$ where $\nu(E) = \int_E \mathbb{1}_{x\geq0}d\mu(x)$. Using the notation for a probability distribution where $P_i = (S_i,\Sigma_i,p_i)$, I will call $P_b$ a weakening of $P_a$, iff $S_a \subset S_b$, $\Sigma_a$ is the $\sigma$-algebra induced on $S_a$ by $\Sigma_b$ and $\forall E \in \Sigma_a : p_a(E)=p_b(E)$.
This corresponds to the notion in logic that $X\vee Y$ is a weakening of $X$ (and also of $Y$). This matches up in the sense that the logical proposition corresponding to inclusion of $e$ in $S_b$. $[[e \in S_b]]$ can be written as $[[e \in S_a]] \vee [[e \in S_b\setminus S_a]]$.
It is clear that $B$ is a weakening of $A$. Trying to work out which one was the OP's intent is not really worth the bother. Here, I wish to explain why that solving problems like this by weakening can be problematic, even if in this particular case it works out just fine. The problem does not stem from the mathematical details of measure theoretic probability theory, but lies in the consistency of it's application. The question is, when is it valid to weaken the support? As I said, this is not about the Kolmogorov formalisation or what have you, but about how one should go about using probabilities if your intention is to model real things.
With the weakening there is no constraint on what the added space represents as it comes from outside of the thing you are modelling. For example, if I were modelling radioactive decay time with an exponential distribution, what does a negative decay time mean? The answer is nothing: it's just nonsense. Probabilistic tachyons. Worse than that, it could be instead interpreted to mean something inherently contradictory, actively destroying any further inferences.
The conservative approach is to just avoid weakening all together, and to say that it is bad practice.
Similar arguments exists against (Lebesgue > 0) zero measure sets, and would usually dismiss the "there are complications" argument on the basis that the complications are "how it should be", or more explicitly, a good model should break exactly where it doesn't apply (hence mentioning the need to define $0\log 0$).
These arguments usually depend on some further assumptions, for example, a Bayesian might argue that one is never completely certain of anything, or, if they are being more formal, that you can't affect or obtain measure zero regions by updating - i.e. they are qualitatively different. Other arguments stem from the behaviour of information measures. I've heard quite a few. Personally though, I just like a clear (not just formal) distinction between the ontological claims described by the support, and the epistemological claims described by the measure - I see this as very important for ensuring information theory does not overstep its bounds, and understanding why the popular claim that "everything is information" is so very wrong.
