Interpreting this shear linear transformation

Question

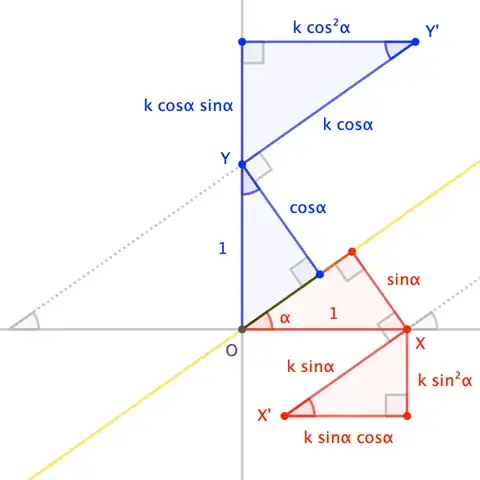
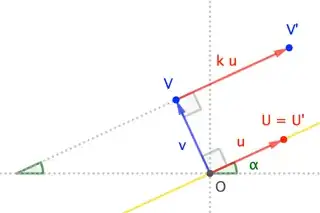
The linear transformation $T$ is a shear which transforms a point $P$ to the point $P'$ defined by

1. $PP'$ makes an acute angle $\alpha$(anticlockwise) with the $x$-axis,
2. $\angle POP'$ is clockwise(i.e. the rotation from $OP$ to $OP'$ clockwise is less than $\pi$)
3. $PP'=k\times PN$ where $PN$ is the perpendicular onto the line $y=x\tan\alpha$ where $k$ is a constant

Show that the matrix representation of $T$ is $\begin{pmatrix} 1-k\sin\alpha\cos\alpha \quad k\cos^2\alpha \\ -k\sin^2\alpha \quad 1+k\sin\alpha\cos\alpha\end{pmatrix}$

I am trying to get my head around this question. I am convinced that $1$ and $3$ are inconsistent. First I drew where a general point $P$ might go, but that didn't work for the same reason my next more promising attempt didn't work. My next attempt was to see where the basis vectors go. Here is my sketch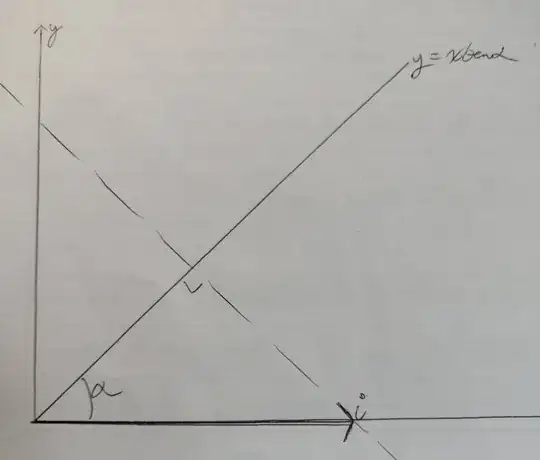 The dotted line is the perpendicular $PN$ produced. $i$ is the basis vector I'm about to transform. By $3$, $P'$ must lie on the dotted line. However, by $1$, the other angle in the triangle must be $\alpha$(In my understanding, the anticlockwise angle with the $x$-axis must be this angle as $PP'$ is parallel to $PN$ produced). But this is simply the assertion that $\alpha=\frac{\pi}{4}$! (which is not in the required answer I have). If I change the line to $y=x\cot\alpha$, it all works out. Does this question have a typo or am I misunderstanding it? Any help is appreciated.

EDIT: Would anyone like to offer an opinion as to why this has not been answered yet? Is it more difficult than it looks or is more information needed on my part to improve the question?

Answer 1

The "required answer" bears-out my suspicion that condition $(3)$ relates the lengths of vectors $PP'$ and $PN$ (as opposed to claiming that one vector is itself a scalar multiple of the other). I commented that signed distances are in play, but the directional information in condition $(2)$ actually allows us to ignore the sign.

In the figure below, $O$ is the origin, and $X$ and $Y$ are points at unit distance along the coordinate axes (corresponding to endpoints of the standard basis vectors), and $X'$ and $Y'$ are their images under this interpretation of the transformation.

We readily compute $$ X' = \left(\begin{array}{c} 1-k\sin\alpha\cos\alpha \\ -k\sin^2\alpha \end{array}\right) \qquad Y' = \left(\begin{array}{c} k\cos^2\alpha \\ 1+k\cos\alpha \sin\alpha \end{array}\right) \tag{$\star$}$$ which match the column vectors of matrix $T$ in the question, as desired. $\square$

---

A now-deleted comment noted that the shear nature of the transformation wasn't clear. That's because the shear is relative to an alternate basis, namely unit direction and normal vectors (say, $u$ and $v$) of the given line.

The figure shows $U$ and $V$ at the endpoints of the vectors, and we see that the transformation fixes $U$ (since its distance from the line is $0$), and it moves $V$ (whose distance from the line is $1$) by distance $k$ in the $u$ direction. Thus, $$T(u) = u \qquad T(v)=ku+v$$ which is how shears work.