Equation of conic section in polar coordiantes

Question

I was wondering why $$\rho(\theta) = \frac{1}{1+e\cos(\theta-\theta_0)}$$ represents a conic in polar coordinates with focus at the origin. There's a canonical way to approach the problem starting from this definition of conic section? In other words starting from $ax^2 +bxy +cy^2+dx+ey +f = 0$.

Answer 1

The second-degree equation $Ax^2+Bxy+Cy^2+Dx+Ey+F=0$ corresponds to a conic in general position. Moving its focus to the origin imposes certain relations on the coefficients that can be difficult to describe.

It's easier to start with the definition that a (non-circle) conic is the locus of a point whose distance to a given point (the focus) is a constant (the eccentricity) times its distance to a given line (the directrix).

$$\text{distance to focus} = \text{eccentricity} \cdot \text{distance to directrix} \tag{0}$$

---

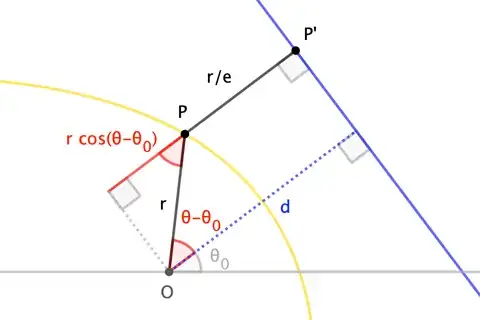
In the figure, $O$ is the focus, $P$ is the point on the conic, and $P'$ is the projection of $P$ onto the directrix, the line at distance $d$ from $O$ whose normal makes an angle $\theta_0$ with the $x$-axis.

Writing $r$ for $|OP|$ and $\theta$ for the angle $\overline{OP}$ makes with the $x$-axis (that is, taking $(r,\theta)$ to be the polar coordinates of $P$), we have $$d = \frac{r}{e}+r\cos(\theta-\theta_0) \quad\to\quad r = \frac{de}{1+e\cos(\theta-\theta_0)} \tag{1}$$ It's customary to replace $de$ with, say, $\ell$ for the length of the semi-latus rectum (the length $r$ when $\overline{OP}$ is parallel to the line; ie, when $\theta-\theta_0=90^\circ$). $$r = \frac{\ell}{1+e\cos(\theta-\theta_0)} \tag{2}$$ This allows the formula to apply to circles, as well. $\square$

---

For the corresponding Cartesian formulation, we square relation $(0)$ and write $$x^2+y^2=e^2 \left(x\cos\theta_0+y\sin\theta_0-d\right)^2 \tag{3}$$ Expanding and re-arranging, we have $$\begin{align} 0 &= x^2(1-e^2\cos^2\theta_0)+y^2(1-e^2\sin^2\theta_0)-2xye^2\sin\theta_0\cos\theta_0 \\ &\quad+2xde^2\cos\theta_0+2yde^2\sin\theta_0 -e^2d^2 \end{align} \tag{4}$$ Again, we can replace $de$ with semi-latus rectum $\ell$ to get a version that works with circles: $$\begin{align} 0 &= x^2(1-e^2\cos^2\theta_0)+y^2(1-e^2\sin^2\theta_0)-2xye^2\sin\theta_0\cos\theta_0 \\ &\quad+2xe\ell\cos\theta_0+2ye\ell\sin\theta_0 -\ell^2 \end{align} \tag{5}$$ I should note that multiplying-through by some arbitrary (non-zero) constant scales the coefficients of $(5)$ without affecting the conic itself. Accordingly, when comparing the general second-degree equation $Ax^2+Bxy+Cy^2+Dx+Ey+F=0$, we have to allow for the constant, say $k$, so that $A=k(1-e^2\cos^2\theta_0)$, $C=k(1-e^2\sin^2\theta_0)$, etc. This adds some complexity to retrieving the geometric parameters from the coefficients; see, for instance, this answer.

Answer 2

Let's set $\theta_0=0$, since rotations preserve the quadratic form for conic sections. Then, you can see this quickly by rewriting the equation to $$ r = \frac{1}{1+ex/r}$$ which gives $$ r+ex=1.$$ Separating $r$ and squaring gives $$ x^2 +y^2 = 1 - 2ex + e^2 x^2$$ i.e. $$ (1-e^2) x^2 + y^2+2ex+1=0.$$ The discriminant is $4(e^2-1)$, which recovers the classification of conic sections.

Note that the squaring also allows for the other branch of the hyperbola.

Edit: of course, this does not explain the fact that the focus is in the origin.