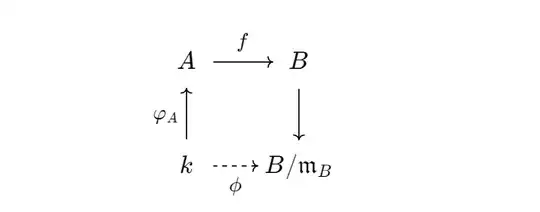Let $k$ be a field. Then $(k,\text{id}_k)$ is a $k$-algebra. Let two further $k$-algebras $(A,\varphi_A)$ and $(B,\varphi_B)$, such that both are local as rings, and a $k$-algebra homomorphism $f:A\rightarrow B$, i.e. $\varphi_B=f\circ\varphi_A$, be given.
Assume that the induced ring homomorphism $q:k\rightarrow B/\mathfrak{m}_B$ is a bijection. Here $\mathfrak{m}_B$ denotes the maximal ideal of $B$.
Now I have to show that $f$ is actually a local ring homomorphism.
I am having trouble doing this! My idea was to show that $\mathfrak{m}_A$ will be mapped to the zero element in $B/\mathfrak{m}_B$ under the composition$A\rightarrow B\rightarrow M/\mathfrak{m}_B$, but I don't know how.
Any help/ hint/ advice is appreciated!