2

Apparently there is a nice theorem related to the anticenter of a cyclic quadrilateral that is not mentioned in the wikipedia:

enter image description here

Anticenter of the cyclic quadrilateral, the intersection point of its diagonals and two intersection points of the lines that contain its opposite sides are always concyclic.

illustration Points E, F, G, H belong to a circle. Can you prove it?

Geogebra sketch.

Jean Marie
  • 81,803
A Z
  • 117
  • 3
    Are you asking for a proof because you have none, or do you have already one ? – Jean Marie Jun 04 '21 at 13:21
  • Good question. I do no have a proof at this moment. Supposedly the proof can be either too easy (so that I probably should be ashamed for asking it) or a bit more complex... Perhaps this book Honsberger, R. Episodes in Nineteenth and Twentieth Century Euclidean Geometry. pp. 36-37 can shed some light on this problem. – A Z Jun 04 '21 at 13:47
  • Still I am surprised that this rather simple observation is not reflected in the online math sources. However on the other hand, the theorem likely should have been known at least to the person who invented the concept of the anticenter.
    There is a simple way to check whether a point or a circle related to a triangle is new or not. For instance, X(1116) = CENTER OF THE LESTER CIRCLE. Is there a similar database for special points related to the quadrilaterals?     – A Z Jun 04 '21 at 13:56
  • P.S. I glanced through "Episodes in Nineteenth and Twentieth Century Euclidean Geometry" (apparently it is the only book that describes the concept of anticenter) and this theorem is not mentioned there: https://archive.org/details/episodes-in-nineteenth-and-twentieth-century-euclidean-geometry-ross-honsberger/page/36/mode/2up So this might be a new theorem. – A Z Jun 04 '21 at 14:14
  • Do you know there is a more general definition of the anticenter ? I cite: "For general cyclical quadrilaterals the reflection of the circumcenter across the centroid is called the anticenter": see p. 7 of this document "Exploring Cyclic Quadrilaterals With Perpendicular Diagonals", Alfinio Flores, University of Delaware, North American GeoGebra Journal Volume 4, Number 1, ISSN 2162-3856. Does this concyclicity property still hold (I mean in the case the quadrilateral is non bicentric) ? – Jean Marie Jun 04 '21 at 14:40
  • no, I didn't know that. The concyclicity property still holds for a case of a cyclic quadrilateral: https://www.geogebra.org/geometry/kshpghc6 – A Z Jun 04 '21 at 15:14
  • Happy to have contributed to a larger theorem... still to be established... – Jean Marie Jun 04 '21 at 15:28
  • I see you have modified your question (no need for the quadrilateral to be bicentric) Permit me to include your figure (under a still form... so keep your Geogebra animation) that will hopefully attract some more people. – Jean Marie Jun 04 '21 at 16:07
  • yes, sure. you can edit the post as needed. – A Z Jun 04 '21 at 16:11
  • A possible track is by using Brocard's (not Brokard's !) theorem as recalled on page 3 of this document http://alexanderrem.weebly.com/uploads/7/2/5/6/72566533/projectivegeometry.pdf – Jean Marie Jun 04 '21 at 19:58
  • 1
    so according to Brocard's theorem R is the orthocenter of the triangle EHF. Point G must be a known triangle center of the triangle EHF as well. – A Z Jun 04 '21 at 20:33
  • It is possible... – Jean Marie Jun 04 '21 at 20:34
  • The anticenter is as well mentionned here. – Jean Marie Jun 05 '21 at 12:50
  • This result dates back to at least 1878/79. See The circle N'N"N"' also goes through Hon pg 254 of https://www.jstor.org/stable/pdf/1967118.pdf, and the reference to a paper by Kantor. This translates in your case to The circle EFH also goes through G – brainjam Sep 16 '21 at 14:00
  • There is an ETC-like database for quadrilaterals etc: Encyclopedia of Quadri-Figures. You can search for anticenter there. See also Clawson Point. In the JSTOR reference in the previous comment it is called the orthic center – brainjam Sep 16 '21 at 14:10

1 Answers1

5

Here is an "ugly" but straightforward solution with complex numbers. $WLOG$, assume $(ABC)$ to be the unit circle. Let $T$ be the anticenter and $X$ be the intersection of the diagonals of the quadrilateral $ABCD$. Lowercase letters denote the affixes.

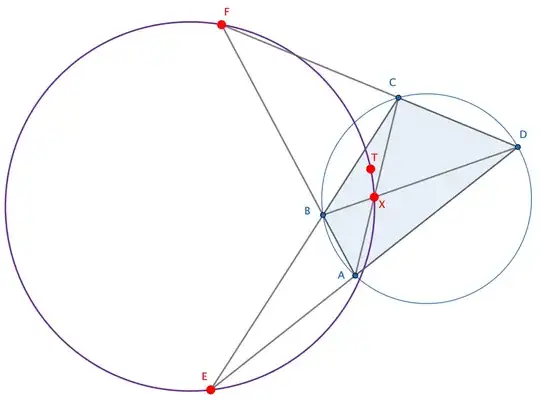enter image description here $\\$

Since the anticenter is symmetric to the circumcenter in the centroid: $$t=\frac{a+b+c+d}{2}$$

The intersection of $AB$ and $CD$ is given by:

$$f=\frac{(\bar{a} b-a \bar{b})(c-d)-(a-b)(\bar{c} d-c \bar{d})}{(\bar{a}-\bar{b})(c-d)-(a-b)(\bar{c}-\bar{d})}$$

Since $|a|=|b|=|c|=|d|=1$, this simplifies to:

$$f=\frac{a b(c+d)-c d(a+b)}{a b-c d}$$

Similarly:

$$e=\frac{a d(c+b)-c b(a+d)}{a d-c b} \; \; \text{and} \; \; x=\frac{a c(b+d)-b d(a+c)}{a c-b d}$$

It is not hard to show that $T, F, E, X$ are concyclic iff:

$$\frac{f-t}{e-t} \div \frac{f-x}{e-x} \; \in \; \mathbb{R} $$

Therefore, we need to show that:

$$\huge{ \frac{\frac{\frac{a b(c+d)-c d(a+b)}{a b-c d}-\frac{a+b+c+d}{2}}{\frac{a d(c+b)-c b(a+d)}{a d-c b}-\frac{a+b+c+d}{2}}}{\frac{{\frac{a b(c+d)-c d(a+b)}{a b-c d}-\frac{a c(b+d)-b d(a+c)}{a c-b d}}}{{\frac{a d(c+b)-c b(a+d)}{a d-c b}-\frac{a c(b+d)-b d(a+c)}{a c-b d}}}}\; \in \; \mathbb{R}}$$

To show this, we can substitute $\frac{1}{a}$ for $a$, $\frac{1}{b}$ for $b$, $\frac{1}{c}$ for $c$, $\frac{1}{d}$ for $d$ (recall $z\bar{z}=1$ for the unit circle), then show that the new expression is equal to the original one (since $z$ is a real number iff $z + \bar{z}=0$). Using Mathematica shows that the two expressions are equivalent. $ \; \; \blacksquare$

Here is what I checked in Mathematica.


True === FullSimplify[((((1/a)*(1/b)*((1/c)+(1/d))-(1/c)*(1/d)*((1/a)+(1/b)))/((1/a)*(1/b)-(1/c)*(1/d))-(((1/a)+(1/b)+(1/c)+(1/d))/(2)))/(((1/a)*(1/d)*((1/c)+(1/b))-(1/c)*(1/b)*((1/a)+(1/d)))/((1/a)*(1/d)-(1/c)*(1/b))-(((1/a)+(1/b)+(1/c)+(1/d))/(2))))/((((1/a)*(1/b)*((1/c)+(1/d))-(1/c)*(1/d)*((1/a)+(1/b)))/((1/a)*(1/b)-(1/c)*(1/d))-(((1/a)*(1/c)*((1/b)+(1/d))-(1/b)*(1/d)*((1/a)+(1/c)))/((1/a)*(1/c)-(1/b)*(1/d))))/(((1/a)*(1/d)*((1/c)+(1/b))-(1/c)*(1/b)*((1/a)+(1/d)))/((1/a)*(1/d)-(1/c)*(1/b))-(((1/a)*(1/c)*((1/b)+(1/d))-(1/b)*(1/d)*((1/a)+(1/c)))/((1/a)*(1/c)-(1/b)*(1/d)))))==(((a*b*(c+d)-c*d*(a+b))/(a*b-c*d)-((a+b+c+d)/(2)))/((a*d*(c+b)-c*b*(a+d))/(a*d-c*b)-((a+b+c+d)/(2))))/(((a*b*(c+d)-c*d*(a+b))/(a*b-c*d)-((a*c*(b+d)-b*d*(a+c))/(a*c-b*d)))/((a*d*(c+b)-c*b*(a+d))/(a*d-c*b)-((a*c*(b+d)-b*d*(a+c))/(a*c-b*d))))]

More detailed explanations of the formulas I used can be found in Evan Chen's this article.

Jean Marie
  • 81,803
krazy-8
  • 2,224