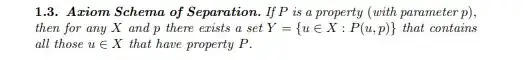I'm reading about the axioms of set theory (from Jech), and I'm having some confusion. There are various parts where it talks about well-formed formulas that include a parameter $p$.
This appears here:
Also here:
Why do we need to include $p$? Couldn't I have just written $\varphi(x, y)$ instead of $\varphi(x, y, p)$?
What kind of parameter is it anyways? Is it a natural number that you plug in? These are very basic questions, but I genuinely don't understand.
I think it may help to see a specific (if rather boring) application. For example, suppose we want to show the following:
$(*)\quad$ For every $p$ and every set $A$, the class $$\{\{a, p\}: a\in A\}$$ is a set.
This is a variant of the argument that for every set $A$ the class $\{\{a\}: a\in A\}$ is a set.
The $p$ above enters the Replacement scheme as a parameter: the result $(*)$ follows from the instance of replacement corresponding to the three-variable formula $$\varphi(x,y,z)\equiv y=\{x,z\}$$ (or a bit more precisely, "$\forall u(u\in y\leftrightarrow u=x\vee u=z)$"), since this instance says exactly "For all $A$ and all $p$ the class of $y$ such that for some $x\in A$ we have $\varphi(x,y,p)$ is a set."
Now it turns out that we ultimately don't need to include parameters in our axioms after all - see here. But this is a very nontrivial and context-specific result; "morally speaking," it is important to include parameters in the Separation and Replacement axioms.
