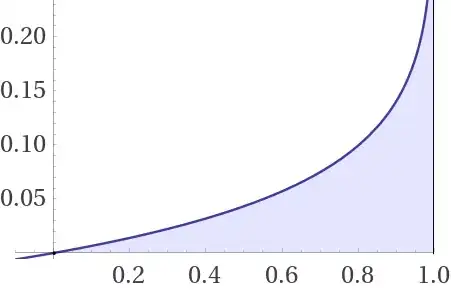
The Nome $\text q(x)$ is definable through Q-Series:
$$\int_0^1\text q(x)dx=\int_0^1 e^{-\frac{π\text K(1-x)}{\text K(x) }}dx=\sum_{n=0}^{\infty} \frac{(-1)^nπ^nK^n(1-x)}{n!K^n(x)}dx=0.060860715078138363199942073390619015335823438347395182336964683032460302197228326471115422640020296331532494217887474046870237415480988255536107139568…$$
$0\le \text q(x)\le1 $:
This has definition for the Nome when Mathworld gives one definition and the other gives the one above using the Complete Elliptic Integral of the First Kind. This integral is similar to here with more information about the Dedekind Eta function.
Progress:
After some help from @Paramanand Singh, this result came up. Note the Jacobi Theta functions $\vartheta_n(0,q)=\vartheta_n(q)$ and the Q-Pochhammer Symbol $(a,b)_n,(a,a)_n=(a)_n$:
$$\int_0^1 \text q(x)dx=\int_0^1\frac{\vartheta_2^4(x) \vartheta_4^4(x)}{ϑ_3^4(x)}dx=\int_0^1 \left[\frac{2\sqrt[4]x\prod_{n=1}^\infty(1-x^{2n}(1+x^{2n})^2\prod_{n=1}^\infty(1-x^{2n})(1-x^{2n-1})^2}{\prod_{n=1}^\infty(1-x^{2n})(1+x^{2n-1})^2}\right]^4dx=16\int_0^1 x\left[\prod_{n=1}^\infty\frac{(1+x^{2n})^2(1-x^{2n})(1-x^{2n-1})}{(1+x^{2n-1})^2}\right]^4dx=16\int_0^1 x\left[\frac{(x+1)^2(-1,x^2)_\infty^2\left(\frac 1x,x^2 \right)_\infty^2(x^2,x^2)_\infty}{4(x-1)^2\} \left(-\frac 1x,x^2 \right)_\infty^2 }\right]^4dx=\frac 1{16}\int_0^1\frac{x(x+1)^8(-1,x^2)_\infty^8\left(\frac 1x,x^2\right)_\infty^8(x^2)_\infty^4}{(x-1)^8 \left(-\frac 1x,x^2\right)_\infty^8}dx$$
Another form with Inverse Nome: $$\int_0^1 \text q(x)dx =1-\int_0^1q^{-1}(x)=1-\int_0^1 \frac{\vartheta_2^4(x)}{\vartheta_3^4(x)}dx=1-16 \int_0^1 x \prod_{n=1}^\infty \left(\frac{x^{2n}+1}{x^{2n-1}+1}\right)^8=1-16\int_0^1 \frac{(-1,x^2)_\infty^8}{\left(\frac 1x, x^2\right)_\infty^8}dx$$
Technically, the integral has a Maclaurin expansion, but there is no compact form with summation notation for the series coefficients. This idea can be seen with the nome expansion and its inverse’s series. Simply using coefficients for the (inverse) nome expansion will not be a sufficient answer, the coefficients for the series should be explicitly or implicitly written. Note that the Inverse Nome is also called the Elliptic Modulus.