I often read that projections are Open but generally not closed. Unfortunately I do not have a counterexample for not closed available. Does anybody of you guys have?
Asked
Active
Viewed 574 times
2
-
What is the exact meaning of projection here? – 23rd Jun 09 '13 at 10:51
-
I think he means projection on a factor of a product space, equipped with the product topology. – Edoardo Lanari Jun 09 '13 at 11:21
-
Note that a projection along a compact set is closed. It is, in fact, equivalent to compactness. It's also used to define notions analogous to compactness in other contexts, such as the completeness of an algebraic variety. – tomasz Jun 10 '13 at 01:41
2 Answers
5
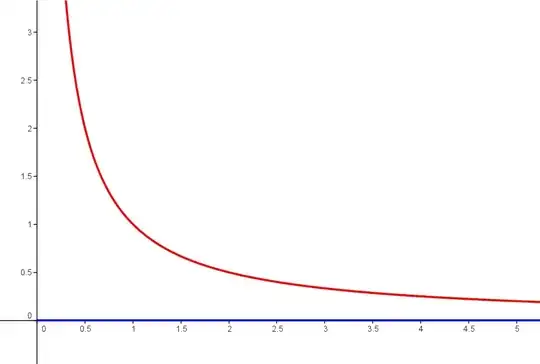
Take the projection in $\Bbb R^2$ onto the first coordinate. Consider the image of the graph of $y=1/x$.
David Mitra
- 74,748
0
The example which is mentioned by David Mitra shows that the projections are not closed:
The projection $p: \mathbb R^2 \rightarrow \mathbb R$ of the plane $ \mathbb R^2 $ onto the $x$-axis is not closed. Indeed, the set $\color{red}{F}=\{(x,y)\in \mathbb R^2 : xy=1\}$ is closed in $\mathbb R^2 $ and yet its image $\color{blue}{p(F)}= \mathbb R \setminus \{0\}$ is not closed in $\mathbb R$.
Paul
- 20,553
-
What's the point of putting another answer that says essentially the same thing as the other one? If you wanted to add the graph, you could have added it to David Mitra's answer, as it is CW anyway... – tomasz Jun 10 '13 at 01:45