Square rooting in tetration.

Question

I have been interested in tetration for a while and I have this question: what is the tetration-root of $2$? ($x^x=2$). In tetration form, it can be written as 2^^x. In general, I am just curious on how to find the tetration-root of any number. i.e. $x^x=a$. Is there is an infinite formula, product, or Taylor series for this type of equation?

Answer 1

$x \approx1.55961046946236935$ has $x^x =2$.

You could say $x = e^{W(\log_e 2)}$, where $W()$ is the Lambert W function with $w=W(z)$ when $we^w=z$

For $x^x = a$,

• when $a >1$ you can replace the $2$ with $a$ so $x = e^{W(\log_e a)}$

• when $e^{-1/e} \lt a \le 1$ there are two non-negative real roots corresponding to the two branches of the Lambert W function

• when $a= e^{-1/e}$ there is one root, namely $x=e^{-1}$

Answer 2

There also exist higher super square roots. Simply go that section in this Wikipedia article. In general, on can solve for $x^x=y$ for y using what is called the “super square root: $$\mathrm{y=x^x\implies x=\sqrt{y}_s=ssrt(y)=e^{W(ln(x))}=\frac{ln(x)}{W(ln(x))}}$$

where W(x) is the Product Logarithm, W-Lambert, Function.

Replace the index of the implied 2 in the surd part with n and you will get the made up inverse of the other function.

It can also be noted that: $$\mathrm{x^{x^…}=y\implies x=y^{1/y}=\sqrt[\infty]{y}_s}$$

This means that the answer of inserting y=2 has, like another answer said. The answer of: $$\mathrm{\mathrm{y=x^x\implies x=\sqrt{2}_s=ssrt(2)=e^{W(ln(2))}=\frac{ln(2)}{W(ln(2))}}= 1.55961046946236934997038876876500299328488351184309142=a...\implies a^a=2}$$

Also, here is a desmos answer to see this graphically: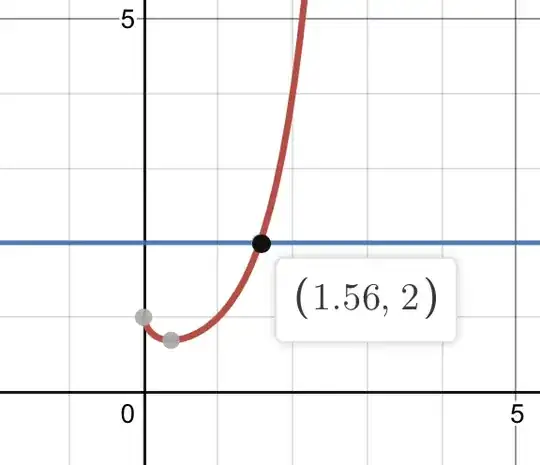

However, there also exist other solutions using different branches of the predefined W(x) function with the link. Software is better explaining than I am. Here are the other solutions with the other branches as its inverse is a relation unless modified.