Given the particular ruler compass construction, prove that GKJHI is a regular pentagon

Question

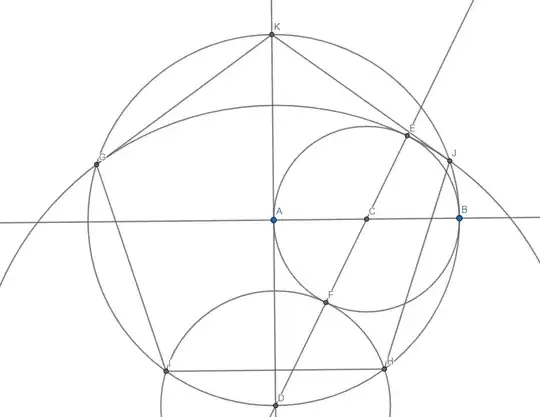
I can show that GK = GJ and GI = GH by drawing the segments from the pentagon vertices to D and using the fact that DK is a diameter. I'm having trouble showing that GK = GI = IH.

Answer 1

If $AB=1$, then $AC=CB=CE=CF=\frac12$ and by Pythagoras, $$DC=\frac{\sqrt5}{2},$$ so $$DH=DI=DF=\frac{\sqrt5 -1}2$$ and $$DG=DJ=DE=\frac{\sqrt5 +1}2.$$ Recall that $$\sin 3\alpha = 3\sin\alpha-4\sin^3\alpha$$ Applying this to $\alpha=\frac12\angle DAH$, for which $\sin \alpha=\frac12DH=\frac{\sqrt 5-1}4$, we find after some computation $$\sin 3\alpha=\frac{\sqrt 5+1}{4}=\frac12DJ $$ and conclude $$ \frac12\angle DAJ=\frac32\angle DAH $$ so that $$\angle HAJ=\angle DAJ-\angle DAH=2\angle DAH=\angle IAH $$ and therefore $$ HJ=IH.$$

---

In a similar fashion, you can use $$ \sin 5\alpha = 5\sin \alpha-20\sin ^3\alpha+16\sin^ 5\alpha$$ to complete the result.