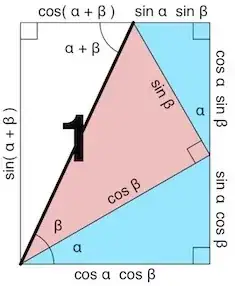
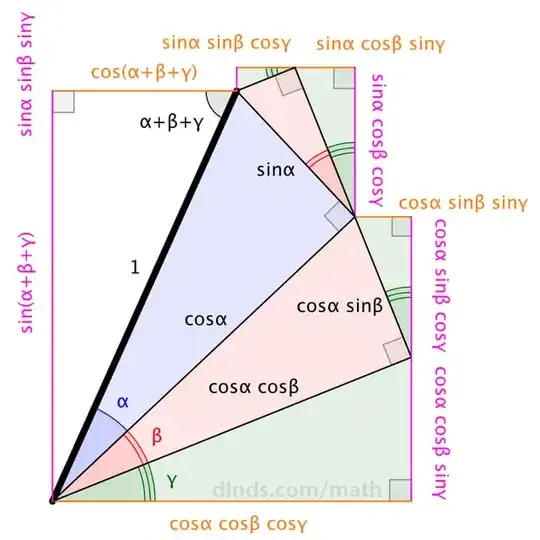
There is no derivation I could find anywhere, and is rarely discussed online.
$\sin(A+B+C+\ldots)$ is what is referred as multi-angle sum not $\sin(3x)$ or $\sin(8x)$, as its finite.
$\sin(\theta_1+\theta_2+\theta_3+\ldots)=\cos(\theta_1)\cos(\theta_2)\cos(\theta_3)\cdots(s_1-s_3+s_5-s_7+\ldots)$
where
$s_n=\sum_{\rm cyc}\tan(\theta_1)\tan(\theta_2)\tan(\theta_3)\cdots\tan(\theta_n)$.
https://brilliant.org/wiki/expansions-of-certain-trigonometric-functions/
The key idea is to use Euler's formula for one angle $$ e^{i\theta}=\cos(\theta)+i\sin(\theta)= \cos(\theta)(1+i\tan(\theta)). \tag{1} $$ Thus, for several angles let $\,\theta:=\theta_1+\theta_2+\dots+\theta_n.\,$ Then let $$ E:=e^{i\theta_1} e^{i\theta_2}\cdots e^{i\theta_n}= e^{i\theta}=\cos(\theta)+i\sin(\theta). \tag{2}$$ From equations $(1)$ and $(2)$ get $$ E \!=\! \cos(\theta_1)\!\cos(\theta_2)\cdots\cos(\theta_n) (1\!+\!i\tan(\theta_1))(1\!+\!i\tan(\theta_2))\cdots(1\!+\!i\tan(\theta_n)) . \tag{3}$$ Expand equation $(3)$ and separate the real and imaginary parts to get $$ \cos(\theta) = \cos(\theta_1)\cos(\theta_2)\cdots\cos(\theta_n) (e_0-e_2+e_4-\dots) \tag{4} $$ and $$ \sin(\theta) = \cos(\theta_1)\cos(\theta_2)\cdots\cos(\theta_n) (e_1-e_3+e_5-\dots) \tag{5} $$ where the $\,e_n\,$ are the $n$-th elementary symmetric polynomials of the tangents.
Not a formal answer, but something to consider ...
Compare these trigonographs for the angle-sum formulas involving two and three angles:
It may not be difficult to convince yourself that, for an arbitrary number of angles, the horizontal sides of the diagram (which combine to make the cosine of the total angle) are labeled with all (and only) those products involving an even number of sines of individual angles. Likewise, the vertical sides (for the sine of the total angle) are labeled with products involving an odd number of sines.
That the groupings should be alternately added and subtracted may not be immediately obvious (especially after just two cases), but this might also not take too much convincing.
