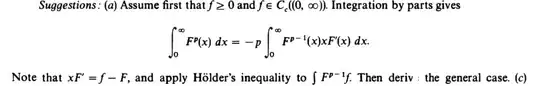I got stuck at two points: I followed the hint and easily proved the case when $f$ is non-negative and compact supported. Then I want to show that for every compact supported $f$ ($f$ can take negative values) the inequality holds. I tried: write $f=f^+-f^-$ we have $||f||_{p}^p=||f^+||_{p}^p+||f^-||_{p}^p$, but how to deal with the integral $F(x)$? This is the first point I got stuck. After solving this, since $C_c(\mathbb{R}^+)$ is dense in $L^p(\mathbb{R}^+)$ with $L^p$ norm, for any $f \in L^p(\mathbb{R}^+)$, we can take $f_n \in C_c(\mathbb{R}^+)$ such that ${f_n}$ tend to $f$ and let $F_n(x):=\frac{1}{x} \int_{0}^{x} f_n(t)dt$.
I have trouble showing that $F_n \rightarrow F$ (in $L^p$ norm):I write down the formula and use Fubini's Thm but the integral tends to infinity, it requires a more precise scaling. Can anyone help me with this exercise? Thanks in advance.
Asked
Active
Viewed 79 times
1
Arctic Char
- 16,007
user725757
- 359
-
1This was asked an answered here. The best constant in the inequality was treated here – Mittens May 24 '21 at 18:39
-
Actually I want a solution following that hint. Another approach is OK. – user725757 May 25 '21 at 02:22