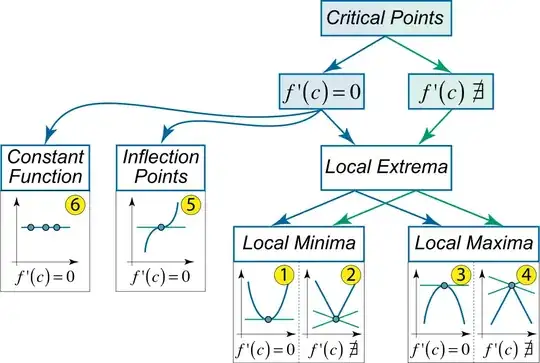
For a cubic $ax^3+bx^2+cx+d$, the radicand of the derivative is $b^2-3ac$ and I was wondering if there's a word for this term. I know that the nature of it being positive, zero, or negative will affect how many critical points the cubic has... but is there a name for this?
Also, based on this answer, there are only 6 possibilities? For each positive or negative $a$ value, then there are three possibilities for the "discriminant" (of the derivative)
You may say (an equation for) stationary points or crtical points.
The discriminant for a cubic is
$$-27 a^2 d^2 + 18 a b c d - 4 a c^3 - 4 b^3 d + b^2 c^2$$
For $n$-th order polynomial equation,
$$\Delta=a^{2n-2} \prod_{i<j} (\alpha_i-\alpha_j)^2=(-1)^{n(n-1)/2}a^{2n-2} \prod_{i \ne j} (\alpha_i-\alpha_j)$$ where $\displaystyle f(x)=a\prod_{i=1}^n (x-\alpha_i)$.
Further points to be noticed
Note that for a polynomial equation beyond linear, there exists at least one global extremum or one inflection point.
$\displaystyle \frac{\sqrt{b^2-3ac}}{3a} \in \mathbb{C}$ in general, relates to linear eccentricity of Steiner in-ellipse of the roots.
Please refer to my post here.
The quantity $b^2-3ac$ does not tell the number of real roots, and I don't think it has a name.
The discriminant of a cubic, which does tell that number ($1,2$ or $3$) is
$$18abcd-4b^3d+b^2c^2-4ac^3-27a^2c2.$$