3

The root $a=-1.191237\dots$ of the polynomial $$P=200000 a^{14} + a^{13} \left(- 340000 t^{3} + 3300000 t - 800000\right) + a^{12} \left(1241000 t^{3} - 1350000 t^{2} - 12075000 t + 13650000\right) + a^{11} \left(- 7348000 t^{3} + 4499000 t^{2} + 69876000 t - 42035000\right) + a^{10} \left(17785750 t^{3} - 14172000 t^{2} - 167986250 t + 131909000\right) + a^{9} \left(- 35837175 t^{3} + 25526125 t^{2} + 338456625 t - 239087875\right) + a^{8} \left(48037075 t^{3} - 35278500 t^{2} - 454618625 t + 333445000\right) + a^{7} \left(- 47826050 t^{3} + 34426200 t^{2} + 453559450 t - 328578000\right) + a^{6} \left(34254150 t^{3} - 24618850 t^{2} - 325370850 t + 236356350\right) + a^{5} \left(- 17669250 t^{3} + 12736700 t^{2} + 167836650 t - 121882300\right) + a^{4} \left(6468960 t^{3} - 4701465 t^{2} - 61045600 t + 44354575\right) + a^{3} \left(- 1647255 t^{3} + 1228155 t^{2} + 15239325 t - 11088125\right) + a^{2} \left(278315 t^{3} - 229280 t^{2} - 2487865 t + 1821840\right) + a \left(- 28860 t^{3} + 24200 t^{2} + 237140 t - 174000\right) + 1324 t^{3} - 1264 t^{2} - 10020 t + 7440$$ where $t=\tan\frac\pi5$ ($t^4-10t^2+5=0$) is the $x$-coordinate of the circled vertex of the below $D_5$-symmetric unit-distance embedding of the Szekeres snark:

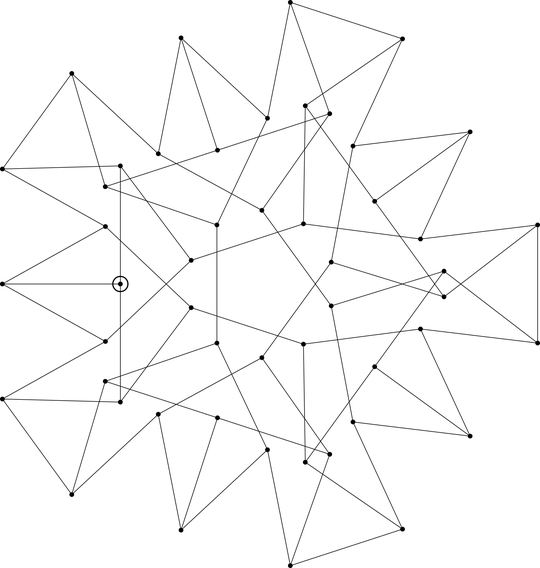
My first reaction upon seeing $P$ was that it had the full Galois group $S_{14}$ over $\mathbb Q[t]$, but the resolvent method would be infeasible for showing this, even probabilistically, as would converting $P$ to a degree-$56$ one over $\mathbb Q$ and running ProbabilityShapes in GAP. Hence I decided to implement Chebotarev's density theorem directly over $\mathbb Q[t]$, but I was confused on how to change the required ingredients in the case where the base field is not $\mathbb Q$ – my question is whether the following work is correct.

I inferred using Lenstra's primer that the application of Chebotarev's in ProbabilityShapes factors a polynomial in $\mathbb Q[x]$ over several primes, tallies the frequencies of each factorisation pattern (the partition of degrees among irreducible factors) and matches them to the frequencies of cycle structures in transitive groups. I think this is what needs to be done when the base field is not $\mathbb Q$:

  • "Factoring $P$ modulo primes" becomes "factoring $P$ modulo prime ideals of the ring of integers of the base field"
  • Only unramified prime (ideal)s should be used; a prime (ideal) is unramified iff $P$'s factorisation modulo it has no multiple factor
  • To obtain the prime ideals in $O_{\mathbb Q[t]}$, factor the ideals generated by integer primes as explained here

All this is encapsulated in the below PARI/GP code:

a; t;
K = nfinit(t^4-10*t^2+5);
poly = 200000*a^14 + a^13*(-340000*t^3 + 3300000*t - 800000) + a^12*(1241000*t^3 - 1350000*t^2 - 12075000*t + 13650000) + a^11*(-7348000*t^3 + 4499000*t^2 + 69876000*t - 42035000) + a^10*(17785750*t^3 - 14172000*t^2 - 167986250*t + 131909000) + a^9*(-35837175*t^3 + 25526125*t^2 + 338456625*t - 239087875) + a^8*(48037075*t^3 - 35278500*t^2 - 454618625*t + 333445000) + a^7*(-47826050*t^3 + 34426200*t^2 + 453559450*t - 328578000) + a^6*(34254150*t^3 - 24618850*t^2 - 325370850*t + 236356350) + a^5*(-17669250*t^3 + 12736700*t^2 + 167836650*t - 121882300) + a^4*(6468960*t^3 - 4701465*t^2 - 61045600*t + 44354575) + a^3*(-1647255*t^3 + 1228155*t^2 + 15239325*t - 11088125) + a^2*(278315*t^3 - 229280*t^2 - 2487865*t + 1821840) + a*(-28860*t^3 + 24200*t^2 + 237140*t - 174000) + 1324*t^3 - 1264*t^2 - 10020*t + 7440;

M = Map();
numpideals = 0;
forprime(p=2,,{
    pideals = idealprimedec(K, p);
    for(i=1, #pideals,
        modP = nfmodprinit(K, pideals[i]);
        p2 = apply(t -> nfmodpr(K, t, modP), poly);
        if(issquarefree(p2),
            numpideals += 1;
            key = apply(poldegree, factor(p2)[,1]~);
            if(mapisdefined(M, key, &count),
                mapput(M, key, count+1),
                mapput(M, key, 1)
            );
            if(numpideals % 1000 == 0,
                print(numpideals, " - ", #M, " cycle types");
                print(M);
            );
        );
    );
});
print(numpideals);
print(M);

After taking into account just $8000$ unramified prime ideals I get

8000 - 107 cycle types
Map([[14], 555; [1, 13], 601; [2, 12], 312; ...])

But the only transitive group on $14$ points with at least $107$ (out of the $135$ possible) cycle types is $S_{14}$:

gap> List([1..NrTransitiveGroups(14)], i->Length(Unique(List(ConjugacyClasses(TransitiveGroup(14, i)), x->CycleStructurePerm(Representative(x))))  ));
[ 4, 3, 5, 5, 6, 3, 8, 5, 6, 5, 5, 5, 6, 7, 6, 8, 10, 10, 9, 9, 5, 7, 8, 9, 8, 9, 9, 8, 10, 6, 12, 14, 10, 8, 
  8, 11, 12, 16, 10, 14, 12, 20, 17, 16, 20, 14, 14, 24, 22, 15, 30, 20, 25, 48, 32, 50, 64, 41, 54, 55, 104, 69, 135 ]

Hence I conclude (and not probabilistically) that $\operatorname{Gal}_{\mathbb Q[t]}(P)=S_{14}$.

Is the conclusion correct? If it is, could I arrive at the conclusion in an easier way?

Parcly Taxel
  • 103,344

1 Answers1

3

Apologies for not answering your exact question, but your strategy does indeed seem sound although I didn't try to read the precise code you wrote.

On the other hand, to prove that a transitive subgroup of $S_n$ is actually $S_n$, it is often helpful to use a little extra group theory. For example, a theorem of Jordan says that a primitive subgroup $G$ of $S_n$ which contains a $p$-cycle for $p < n-2$ then $G = A_n$ or $S_n$. This often allows you to reach your conclusion much quicker than some algorithm which requires enumerating all transitive subgroups of $S_n$ (which for $n$ large is prohibitive).

For example, suppose that $p = 61$. Then

$$(t^4 - 10 t^2 + 5) = (t - 40) \ldots \mod 61,$$

and so $\mathfrak{P} = (t-40,61)$ is a prime in $K = \mathbf{Q}(t)$. Reducing your polynomial modulo this prime, the degree $14$ polynomial has irreducible factors of degrees $1$, $2$, and $11$. From this we deduce:

  1. $G$ is transitive since the original polynomial is irreducible. (Actually, I assumed this was true and you checked it, but it is easy to prove by using the prime $\mathfrak{Q} = (41,t - 15)$ where the Frobenius element is a $14$-cycle.)
  2. $G \subset S_{14}$ contains an element $\sigma$ with cycle shape $1+2+11$.
  3. $G$ contains a $11$-cycle. (Take $\sigma^{2}$).
  4. $G$ is primitive, since no element of order $11$ can preserve any non-trivial decomposition of $14$ elements (uses that $G$ is transitive).
  5. Since $11 < 14 - 2$, $G$ is either $A_{14}$ or $S_{14}$ by Jordan's theorem.
  6. $G = S_{14}$ because $\sigma$ is odd (even $\sigma^{11}$ is a $2$-cycle).

In particular, it's easier to recognize $S_{n}$ (or even $A_{n}$) by finding particular cycle shapes than counting all cycle shapes and comparing with every possible transitive subgroup. What is usually more difficult is identifying the group $G$ when it is not one of these groups --- then the method of computing many cycle shapes and using Cebotarev (or the weaker version of Frobenius) is helpful in identifying the group.

user868719
  • 241