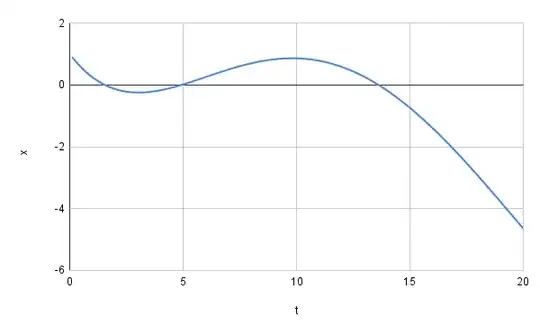
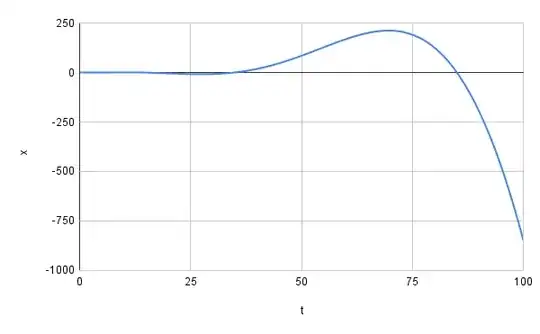
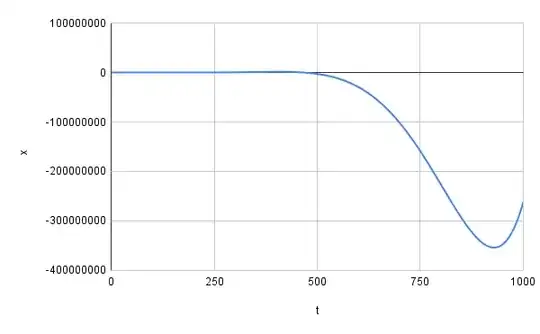
Define the function $x(t)$ for $t\ge0$: $$ x(0)=1\\ x'(t)=-x(t/2) $$ I could do a power series from $t=0$ like this (thanks to @JeanMarie for pointing this old question out), but I ultimately want asymptotic bounds on the excursions as $t\to\infty$, so I don't think the power series helps. Is there any other research on this function? How quickly do these excursions grow with $t$?
