Contour integral $\int_{C_\varepsilon}\frac{e^{i\alpha\omega}}{\omega^2}\mathrm{d}\omega$

Question

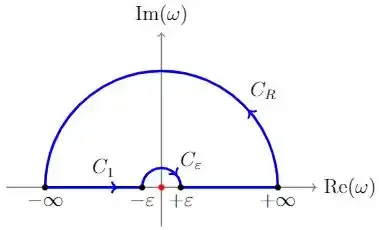
One intermediate step of an exercise requires to evaluate the the following integral with variable $\omega\in\mathbb{C}$, $$ \lim_{\varepsilon\to0^+}\int_{C_\varepsilon}\frac{e^{i\alpha\omega}}{\omega^2}\mathrm{d}\omega \quad\text{with}\quad \alpha>0 \tag{1} $$ where $C_\varepsilon$ is the upper semi-circular arc centered at origin and with radius $\varepsilon\to0^+$. The full contour (indented upper semi-circle) used in this exercise is shown below:

Because the pole of the integrand at $\omega=0$ is not a simple pole (it is of order 2), the corollary to the Jordan's lemma is not applicable. Have tried substituting $\omega=\varepsilon e^{i\theta}$ and Mathematica, I get $$ \begin{aligned} \int_{C_\varepsilon}\frac{e^{i\alpha\omega}}{\omega^2}\mathrm{d}\omega &= \int_\pi^0\frac{\exp{({i\alpha \varepsilon e^{i\theta}})}}{\varepsilon^2 e^{2i\theta}}\varepsilon i e^{i\theta}\mathrm{d}\theta \\ &= \frac{i}{\varepsilon}\int_\pi^0\exp{[i({\alpha \varepsilon e^{i\theta}}-\theta)]}\mathrm{d}\theta \\ &=-\frac{2}{\varepsilon}\cos{(\alpha\varepsilon)} +i\alpha\left[ \mathrm{Ei}(i\alpha\varepsilon)-\mathrm{Ei}(-i\alpha\varepsilon) \right] \end{aligned} \tag{2} $$ where $\mathrm{Ei}(z)$ is the exponential integral function. At the last step I don't know how to proceed, as the function value is of the indeterminate form $\infty+i\infty-i\infty$ as $\varepsilon\to0^+$.

Using regularization method via $\omega^2\to(\omega+i\varepsilon)^2$, I can show that $$ \lim_{\varepsilon\to0^+}\oint_C\frac{e^{i\alpha\omega}}{(\omega+i\varepsilon)^2}\mathrm{d}\omega = 0 \Longrightarrow \oint_C\frac{e^{i\alpha\omega}}{\omega^2}\mathrm{d}\omega = 0 $$ where $C=C_1+C_R$ is the upper semi-circle without the indent at origin. The contour integral $\int_{C_R}=0$ due to Jordan's lemma, and thus $\int_{-\infty}^\infty=0$. With this observation, I believe the integral in (1) should be zero as well, but I don't know how to proceed from (2).

Could anyone provide some hints? Many thanks.

Answer 1

but I don't know how to proceed from (2).

$\omega=0$ is a double pole, therefore $$\lim_{\varepsilon\to0^+}\int_{C_\varepsilon}\frac{e^{i\alpha\omega}}{\omega^2}\mathrm{d}\omega \text{ is divergent}$$ which has also been shown by OP's equation (2). There is really no way to go around a double pole.

---

Could anyone provide some hints? Many thanks.

I guess the OP is trying to evaluate $$\int_{-\infty}^\infty\frac{e^{i\alpha z}}{z^2}\,\mathrm{d}z$$

One may try the Hadamard finite part (denoted as $\mathcal{H}$) which assigns a finite value for the singular integral $$ \mathcal{H}\int_{-\infty}^\infty\frac{e^{i\alpha z}}{(z-t)^2}\,\mathrm{d}z :=\frac{\mathrm{d}}{\mathrm{d}t}\left[\mathcal{P}\int_{-\infty}^\infty\frac{e^{i\alpha z}}{z-t}\,\mathrm{d}z\right] $$ where $\mathcal{P}$ denotes Cauchy principal value. Use the Sokhotski–Plemelj theorem to find $\mathcal{P}$, $$ \mathcal{P}\int_{-\infty}^\infty\frac{e^{i\alpha z}}{z-t}\,\mathrm{d}z = \frac{1}{2}\lim_{\epsilon\to0^+}\Bigg[\underbrace{\int_{-\infty}^\infty\frac{e^{i\alpha z}}{z-t- i\epsilon}\,\mathrm{d}z}_{=2\pi i e^{i\alpha(t+i\epsilon)}}+\underbrace{\int_{-\infty}^\infty\frac{e^{i\alpha z}}{z-t+ i\epsilon}\,\mathrm{d}z}_{=0}\Bigg] =\pi i e^{i\alpha t}\tag{*} $$ where the contour integration with upper semi-circle is used to get the integral values. Therefore, $$ \mathcal{H}\int_{-\infty}^\infty\frac{e^{i\alpha z}}{(z-t)^2}\,\mathrm{d}z =\frac{\mathrm{d}}{\mathrm{d}t}\left(\pi i e^{i\alpha t}\right)=-\alpha\pi e^{i\alpha t} $$ Letting $t=0$, $$ \mathcal{H}\int_{-\infty}^\infty\frac{e^{i\alpha z}}{z^2}\,\mathrm{d}z=-\alpha\pi $$

---

Warning: The Hadamard finite part got its name because it manually drops the divergent terms such as $\lim_{\varepsilon\to0^+}\int_{C_\varepsilon}e^{i\alpha\omega}/\omega^2\,\mathrm{d}\omega$ in this case as no one knows how to deal with the divergent terms. Therefore, one should always refer to the context of the (physical) problem to check if the $\mathcal{H}$ value makes any sense.

---

To reply @zytsang's question in the comment, suppose we know A Priori the result we want: $$\begin{cases} 0 & \quad \text{for}\quad\alpha>0 \\ 2\pi\alpha & \quad \text{for}\quad\alpha<0 \end{cases}$$ Denote $\mathcal{P}'_+$ and $\mathcal{P}'_-$ as the principal-values-as-we-want-it. The regularization in (*) can be manipulated as $$ \mathcal{P}'_+\int_{-\infty}^\infty\frac{e^{i\alpha z}}{z-t}\,\mathrm{d}z =\frac{1}{2}\lim_{\epsilon\to0^+}\Bigg[\underbrace{A\cdot\int_{-\infty}^\infty\frac{e^{i\alpha z}}{z-t- i\epsilon}\,\mathrm{d}z}_{=2\pi i A e^{i\alpha(t+i\epsilon)}}+\underbrace{B\cdot\int_{-\infty}^\infty\frac{e^{i\alpha z}}{z-t+ i\epsilon}\,\mathrm{d}z}_{=0}\Bigg] \quad \text{for }\alpha>0 \text{ (upper semi-circle)} $$ Setting $A=0$ gets the physical result for $\alpha>0$. Similarly, $$ \mathcal{P}'_-\int_{-\infty}^\infty\frac{e^{i\alpha z}}{z-t}\,\mathrm{d}z =\frac{1}{2}\lim_{\epsilon\to0^+}\Bigg[\underbrace{C\cdot\int_{-\infty}^\infty\frac{e^{i\alpha z}}{z-t- i\epsilon}\,\mathrm{d}z}_{=0}+\underbrace{D\cdot\int_{-\infty}^\infty\frac{e^{i\alpha z}}{z-t+ i\epsilon}\,\mathrm{d}z}_{=-2\pi i D e^{i\alpha(t+i\epsilon)}}\Bigg] \quad \text{for }\alpha<0 \text{ (lower semi-circle)} $$ Setting $D=2$ gets the physical result for $\alpha<0$. Because the original integral is divergent, if you are allowed to artificially specify the rate of taking the limit on different directions, you can get whatever you want.

“Divergent series are the invention of the devil, and it is shameful to base on them any demonstration whatsoever.”—N. H. Abel

Although Abel's quote is for divergent series, I think it is also relevant to the divergent integral. But I wouldn't mind the "shameful" part, though.