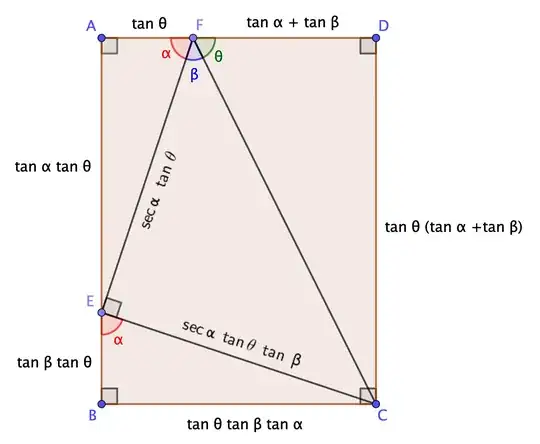
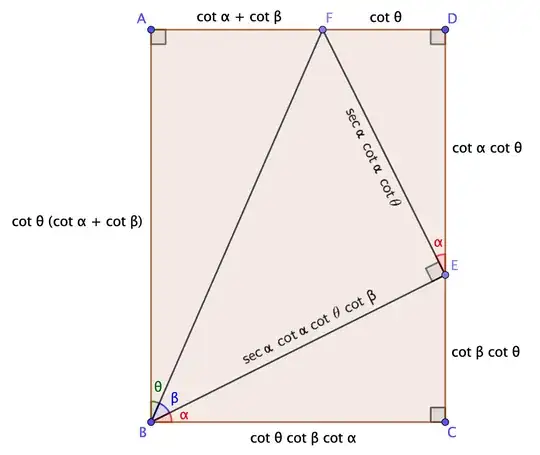
The not-so-well-known triple tangent and triple cotangent identities,
If $x + y + z = \pi$ then $\tan x + \tan y + \tan z = \tan x\tan y\tan z \;\;\; (x,y,z \neq \pi/2+\pi n)$.
If $x + y + z = \frac\pi 2$ then $\cot x + \cot y + \cot z = \cot x \cot y \cot z \;\;\; (x,y,z \neq \pi n)$.
are usually proved analytically. Are there geometric proofs of these identities? Or at least geometric interpretations that might provide some intuition for why they are true?