2

I have a question about the addition formula for $\sin x$ and $\cos x$ . Generally, I have seen the following formula referenced $$a\sin x + b \cos x = \sqrt{a^2+b^2} \cos ( x + \arctan{-\frac{a}{b}})$$ however, this formula seems to only hold for $b>0$ . I have attached an image for $b>0$ and for $b<0$

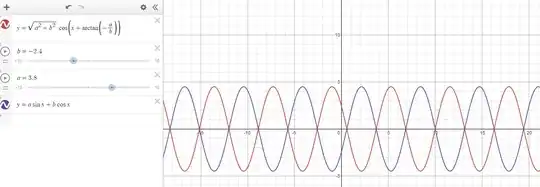enter image description hereenter image description here . First I thought it had something to do with the principle value of $\arctan$ , however, after some experimentation I found that the following to hold for all $a$ and $b$

$$a\sin x + b \cos x =\frac{b}{|b|} \sqrt{a^2+b^2} \cos ( x + \arctan{-\frac{a}{b}}) $$ except for $b=0$. Does anybody know this seems to occur and moreover what is the principled way of dealing with simplifications for $a\sin x + b \cos x$ (when given values and when not)?

Thanks in advance

Maths Wizzard
  • 2,259

1 Answers1

2

The idea of the formula is to find an angle $\theta$ such that $\sin\theta = a/R$ and $\cos\theta = b/R.$ You can then change the phase of the cosine curve by $\theta$ in order to line up the peaks and troughs with your sinusoid $a\sin x + b\cos x.$

The problem is that if $\frac\pi2 < \theta < \frac{3\pi}2$ then $\cos\theta < 0$ and

$$ \arctan\left(\frac{\sin\theta}{\cos\theta}\right) = \theta - \pi. $$

Similarly for any other angle $\theta$ such that $\cos\theta < 0$, the result of $\arctan(\tan\theta)$ will differ from $\theta$ by an odd multiple of $\pi$.

There is also the case where $\theta < -\frac\pi2$ or $\theta > -\frac\pi2$ and $\cos\theta > 0,$ where $\arctan(\tan\theta)$ differs from $\theta$ by an even multiple of $\pi$, but this case doesn't cause any trouble because an even multiple of $\pi$ will give you a sinusoid in phase with your original one.

The problem with the odd multiples of $\pi$ is that they give you a curve $\pi$ radians out of phase, which is the same as flipping the sign of the curve at all points. Multiplying by the sign of $b$ fixes this.

A more complete solution is to write

$$ a\sin x + b \cos x = \sqrt{a^2+b^2} \cos ( x - \operatorname{atan2}(a,b)) $$

where $\operatorname{atan2}$ is the two-parameter arc tangent function. This works not only when $b < 0$ but also when $b = 0.$

David K
  • 98,388