I am new to sequences and encountered a task where I am to show that a sequence $(a_n)$ that fulfills the following criteria is a Cauchy sequence.
$\forall n > 1 : |a_{n+1} - a_n| \leq q \cdot |a_n - a_{n-1}|$ with $0 < q < 1$.
This means that the following is true as well:
$|a_{n+1} - a_n| \leq q^n \cdot |a_1 - a_0|$
$\frac{|a_{n+1} - a_n|}{|a_1 - a_0|} \leq q^n$
$0 \leq \frac{|a_{n+1} - a_n|}{|a_1 - a_0|} \leq q^n$
Since $q^n$ converges to 0, I can use the Squeeze theorem to conclude that the sequence $(a_n)$ converges to 0 as well. Every converging sequence is a Cauchy sequence which concludes my proof.
However, I am really unsure because I also found sequences that look like they would fulfill the description but are not converging like this one: 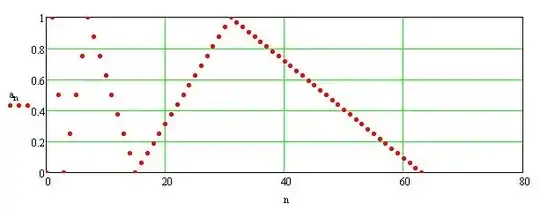
Where did I go wrong and how can I show that it is a Cauchy sequence?
I was made aware of a post dealing with the same problem and using Cantor's lemma: Using Cantor's lemma in a proof of convergence
However, I am not allowed to use Cantor's lemma for this task, so any help would be appreciated.