1

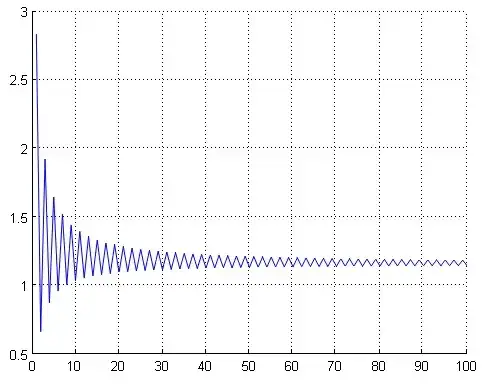
I try to separate the following double sum

$$S=\sum_{i,j \in[-n,n], (i,j)\ne (0,0)} f_{ij}$$

where

$$f_{ij}=\frac{(-1)^{j+k}}{\sqrt{j^2+k^2}}$$

$$S=\sum _{k=1}^n \sum _{j=1}^n (f(-k,-j)+f(-k,j)+f(k,-j)+f(k,j))$$

but I do not know why it does not work for several value of integers.

Could you help to get a formula for n dimensional sum

Thanks

Jean Marie
  • 81,803
user547221
  • 357
  • I try sum lattice sums and I need a general n dimension formula ,it is a way of begining ,Thanks @Jean Marie – user547221 May 16 '21 at 08:10
  • Your title is misleading: as I understand, you look for a closed-form formula... – Jean Marie May 16 '21 at 15:32
  • Yes pleases , in dimension two or three is will be ok – user547221 May 16 '21 at 16:29
  • What do you mean by "change of indices", by "separate" ? Explain with detailed sentences what you want to do. – Jean Marie May 16 '21 at 20:43
  • In order to attract more people, I have changed your expressions which had a hard-to-read "Wolfram Alpha"/Mathematica syntax into their usual mathematics syntax. – Jean Marie May 17 '21 at 08:05
  • 1
    Your last expression is not the right one because you exclude for example indices (k=1,j=0) which should be included. – Jean Marie May 17 '21 at 08:09
  • I think there is an issue about vocabulary: what do you mean when you say "$n$ dimensional sum" ? With terms of the form $\dfrac{(-1)^{a+b+...+n}}{\sqrt{a^2+b^2+...+n^2}}$ ? – Jean Marie May 17 '21 at 11:49

1 Answers1

1

Here is a numerical simulation giving the values of $S$ from $n=1$ to $n=100$.

A convergent behavior takes place with oscillations around a limit $\approx 1.164$.

enter image description here

but I am unable to find its exact value.

Nevertheless, this kind of sum has been studied: it is $b_2(1)$ with $b_2(s)$ given by formula (3), Problem n° 3 in this interesting [document] (https://www.davidhbailey.com//dhbpapers/tenproblems.pdf)

See as well here.

Both documents mention this formula:

$$b_2(s)=-4\beta(s)\zeta(s)$$

which unfortunately is valid only for $s>1$.

Somewhat related: Infinite sum involving number of solutions to $k=i^2+j^2$

Jean Marie
  • 81,803
  • thanks @Jean Marie for the try maybe I express myself really bad what I want , I can calculation de numerical result but this is not the question, the double sum goes fron - Infinity t o infnity I need it is to get a representation of this sum for 0 to infnity for other reasons – user547221 May 17 '21 at 12:34
  • Could you say what you call "to get a representation" ? Is it a "closed-form formula" (see what this expression mean) ? And what do you mean about "n" dimensional sum in your question ? – Jean Marie May 17 '21 at 12:36
  • in Math languaje $$\sum _{k=-n}^n \sum _{j=-n}^n \to \sum _{k=1}^n \sum _{j=1}^n$$ – user547221 May 17 '21 at 18:22
  • 1
    You had asked a question previously a question on Madelung constant : you should link your questions in order to help people to help you. – Jean Marie May 20 '21 at 20:53