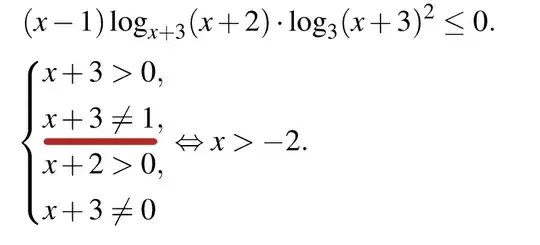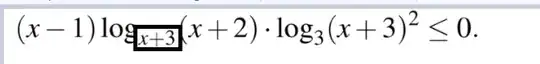1

One step of solve this is :enter image description here

I dont understand, why $x+3\neq1$ ? We solve it with function domain help. If $\log_3(1)^2$ this may exist but not true, and if $x+3\neq2$ may exist but not true. If $\log_{1}(x+2)$ then $(x+2)^0$ is true.

bazylevnik0
  • 61

3 Answers3

1

The base of a logarithm cannot be $1$. So, assuming $$\log_ax$$ is a function of both $a$ and $x$, the domain is $x > 0$ and $a > 0, a\ne 1$.

For more details, check this out.

stoic-santiago
  • 13,705
1

Recall that if $a^b = c$, then $\log_a c = b$ and vice versa. So if $\log_{x+3} (x+2)$ was defined and equalled $u$, there would be some $u$ where $(x+3)^u = (x+2)$, which is absurd.

Alternatively, by the change of base formula, it would equal $\frac{\log(x+2)}{\log (x+3)}$, where $\log(x+3) \ne 0$ to avoid division by $0$, and raising both sides to the power of the given base, $x+3 \ne 1$.

Toby Mak
  • 16,827
1

According to the Logarithm definition the defining relation between exponentiation and logarithm is:

${\displaystyle \log _{b}(x)=y\ }$ exactly if ${\displaystyle \ b^{y}=x\ } and {\displaystyle \ x>0}$ and ${\displaystyle \ b\neq 1}$

Thus base can't be $1$.

However if $x+3=1$ then enter image description here

the part in rectangle in above picture in that the base will become $1$ which contradicts the definition. Thus $a+3$ is not equal to $1$.