Finding the equation of the circle with given radius tangent to lines $y=x$ and $y=2x$ using pencils of circles.

Question

Find the equation of the circle with radius $3$ whose center lies in the first quadrant and is tangent both to the lines $y=x$ and $y=2x$

My solution is as follows

Let $(x_1,y_1)$ and $(x_2,y_2)$ be the points of contact with resp. tangents $y=2x$ and $y=x$:

The two families of circles are

${x^2} - 2x{x_1} + {x_1}^2 + {y^2} - 2y{y_1} + {y_1}^2 + L\left( {y - 2x} \right) = 0 \Rightarrow \\{x^2} + {y^2} - 2x\left( {{x_1} + L} \right) - 2y\left( {{y_1} - \frac{L}{2}} \right) + {x_1}^2 + {y_1}^2 = 0$

&

${x^2} - 2x{x_2} + {x_2}^2 + {y^2} - 2y{y_2} + {y_2}^2 + M\left( {y - x} \right) = 0 \Rightarrow \\{x^2} + {y^2} - 2x\left( {{x_2} + \frac{M}{2}} \right) - 2y\left( {{y_2} - \frac{M}{2}} \right) + {x_2}^2 + {y_2}^2 = 0$

Both circles are similar, how do we equate the values ?

Answer 1

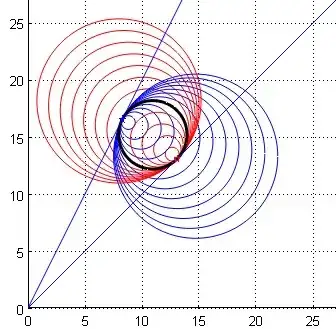
Fig. 1: (Some circles of) the pencil of circles $P_1$ in blue, and $P_2$ in red (notations of (1)). Their common circle, the one we want, is in black. Point-circles $(x_1,y_1)$ and $(x_2,y_2)$ are materialized by small stars.

I understand your method in the following way. You consider two linear pencils of circles each one generated by a "point-circle" [...] and a straight line:

$$\begin{cases}[(x-x_1)^2+(y-y_1)^2]+L(y-2x)&=&0&\text{pencil} \ P_1\\ [(x-x_2)^2+(y-y_2)^2]+M(y-x)&=&0&\text{pencil} \ P_2\end{cases} \tag{1}$$

and you want to find the common circle to the two pencils ; the problem you meet is that, by identification of like coefficients,

$$\begin{cases}x_1 + L&=&x_2+\frac{M}{2}\\y_1 - \frac{L}{2}&=&y_2 - \frac{M}{2}\\x_1^2 + y_1^2&=&x_2^2 + y_2^2\end{cases}\tag{2}$$

you have 3 equations with 6 unknowns...

1. In fact you should use only 4 unknowns because $y_1=2x_1$ and $y_2=x_2$.

2. Moreover you haven't used the fact that the radius is $3$ ; this can be done by expressing that the center of the circle whose coordinates are "visibly" $(x_1+L,y_1-\frac{L}{2})=(x_1+L,2x_1-\frac{L}{2})$ is at distance $3$ from $(x_1,y_1)=(x_1,2x_1)$ ; this condition is expressed by

$$L^2+\frac{L^2}{4}=3^2 \ \implies \ L=\dfrac{6}{\sqrt{5}}\tag{3}$$

(The plus sign has been chosen in order to have the center of the circle under the line with equation $y=2x$ ; we could have as well chosen to determine $M=-3\sqrt{2}$).

$L$ being known, system (2) is reduced to 3 simple equations with 3 unknowns.

In this way your method is fully viable.

Remark: the third equation in (2) expresses the equality of the lengths of the tangents $OT_1$ and $OT_2$ issued from the origin.

---

Here is a different way. Let $C=(x_0,y_0)$ be the center of the circle.

The different constraints of distances can be encapsulated into the double equation (see here):

$$\underbrace{\dfrac{1}{\sqrt{2}}(y_0-x_0)}_{\text{distance from C to line } y-x=0}=\underbrace{\dfrac{1}{\sqrt{5}}(2x_0-y_0)}_{\text{distance from C to line } y-2x=0} \ = \ \ 3$$

whose solution is

$$x_0=3(\sqrt{2}+\sqrt{5}), \ \ y_0=3(2\sqrt{2}+\sqrt{5})$$

Therefore, the equation of your circle is:

$$(x-x_0)^2+(y-y_0)^2=3^2$$

that can be somewhat simplified if you expand the squares.

Answer 2

There could be a better approach. You have been given the lines $y=x$ and $y=2x$. You should just consider coordinates of centre of circle to be $(h,k)$, and then simply write the equation of perpendicular distance from a point on a line, for both given lines. This will give you two relations to solve, thus you get centre's coordinates. While solving be careful to note that centre must lie above $y=x$ but below $y=2x$.

Answer 3

For two given lines that are not parallel to each other, the angle bisector is given by

$ \displaystyle \frac{Ax+By+C}{\sqrt{A^2+B^2}} = \pm \frac{ax+by+c}{\sqrt{a^2+b^2}}$

where the given lines are $Ax + By + C =0$ and $ax + by + c =0$

We have lines $y-2x = 0$ and $y-x = 0$ that intersect at the origin.

$ \displaystyle \frac{y-x}{\sqrt{2}} = \pm \frac{y-2x}{\sqrt{5}}$

For internal bisector,

$ \displaystyle \frac{y-x}{\sqrt{2}} = - \frac{y-2x}{\sqrt{5}}$

$\implies \displaystyle y = \frac{2\sqrt2+\sqrt5}{\sqrt2+\sqrt5} x$

$\displaystyle y = \frac{1+\sqrt{10}}{3} x$

As the center of the circle is on this line, its coordinates can be written as $(x_0, \frac{1+\sqrt{10}}{3} x_0)$.

Now perpendicular distance to $y - x = 0$ from the center is $3$.

$ \displaystyle \frac{|\frac{1+\sqrt{10}}{3} x_0 - x_0|}{\sqrt2} = 3$

Solving $ \displaystyle x_0 = \frac{9\sqrt2}{\sqrt{10}-2} = 3 (\sqrt5+\sqrt2), y_0 = 3 (\sqrt5+2\sqrt2)$

And equation of circle is $(x-x_0)^2 + (y-y_0)^2 = 9$

Answer 4

My approach would be to first put the circle at the origin. Then find where tangent lines of the given slopes interesect, and shift from there.

The circle $x^2+y^2=9$ has tangent lines at $(x,y)$ with slope $-\frac{x}{y}$. So the slope $1$ tangent line is tangent at some $(a,-a)$. So $2a^2=9$, and $a=\frac{3}{\sqrt{2}}$. The point is $\left(\frac{3}{\sqrt{2}},-\frac{3}{\sqrt{2}}\right)$.

The slope $2$ tangent line is tangent at some $(-2b,b)$. So $5b^2=9$, and $b=\frac{3}{\sqrt{5}}$. The point is $\left(\frac{-6}{\sqrt{5}},\frac{3}{\sqrt{5}}\right)$.

So the two lines are $$\begin{align} y&=(x-3/\sqrt{2})-\frac{3}{\sqrt2}=x-\frac{6}{\sqrt2}\tag{EQ1}\\ y&=2(x+6/\sqrt{5})+\frac{3}{\sqrt5}=2x+\frac{15}{\sqrt{5}}\tag{EQ2} \end{align}$$

Solve that system to find where the lines intersect: $$\left(\text{EQ2}-\text{EQ1}\,\text{to find }x,2\text{EQ1}-\text{EQ2}\,\text{to find }y \right)$$ $$\left(-\frac{15}{\sqrt{5}}-\frac{6}{\sqrt{2}},-\frac{15}{\sqrt{5}}-\frac{12}{\sqrt{2}}\right)$$

So with the original question, shift by the negative of the above to get the center: $$\left(\frac{15}{\sqrt{5}}+\frac{6}{\sqrt{2}},\frac{15}{\sqrt{5}}+\frac{12}{\sqrt{2}}\right)$$