7

Let $(X,\mathcal{M})$ and $(Y,\mathcal{N})$ be measurable spaces. We call the function $f:X\to Y$ to be $(\mathcal{M},\mathcal{N})$-measurable if $f^{-1}(E)\in \mathcal{M}$ for all $E\in \mathcal{N}$.

Similarly, when we are trying to define "nearness" in functions we call a function to be continuous if the preimage of the open set is open. There might be other types of similar definitions (if so, I'd appreciate more examples!), but my question is why we define the particular function always based on the preimage?

Thanks in advance!

quuuuuin
  • 637
  • 3
  • 8
  • The useful things about a function $f$ are sets like ${x : f(x)<a}$. For example, these are the sets we need to know about in order to integrate $f$. – GEdgar May 13 '21 at 01:48
  • This isn't the best answer, but the sense I have is that a lot of theory in measure-theoretic stochastic processes simply breaks down with any other definition of measurability. – MathematicsStudent1122 May 13 '21 at 01:50
  • 7
    One reason is that the preimage preserves set operations while the image doesn't so we can carry back set structures (measurable sets, open sets etc) but not forward; for example assuming standard set theory and existence of non measurable lebesgue sets, it is not hard to construct continuous functions that take some measurable lebesgue sets into non measurable ones – Conrad May 13 '21 at 01:50
  • Preimages in some sense allow you to use real-valued functions (which we know a lot about) to tell you things about the set in question. For example, if the set was a large elephant, then a real valued function on the set could be in some sense considered a blind man touching a part of the elephant and getting a value. – rubikscube09 May 13 '21 at 03:05

3 Answers3

5

It's not that we "always" define things in terms of preimages, it's just that the preimage-based definitions are the ones that "do the right thing" in the cases you mentioned.

Measurable functions allow Lebesgue integration because we can partition the range into small disjoint sets, measure the preimages of those sets, and add up the resulting areas. The sum is justified because the preimages of disjoint sets are disjoint; it wouldn't work right if you instead tried to define integration using the "forward" property $E\in\mathcal M\implies f(E)\in\mathcal N$ (but you should try it!).

The situation is more subtle for continuity of functions (see this question), but the familiar $\epsilon/\delta$ definition of continuity in metric spaces is equivalent to the preimage-based definition in terms of open sets.

Karl
  • 11,446
3

Unless we assume injectivity, it is extremely difficult to "control" the image with the preimage. In fact, in the case of a constant map, every nonempty preimage has the same image, so the preimage tells us nothing about the image at all.

Inverse functions are forced to be injective, so we do not have this problem when we try to control the preimage in terms of the image.

user3716267
  • 1,165
1

The measure theory was born from the need to formalize the idea of integration for Lebesgue.
In this context we need of the notion of measurable function for identify the class of function on which successively we could define the notion of integral. In particular, the Lebesgue integral would generalize, in some sense, the Riemann integral.
The idea behind the formal construction of Lebesgue integral is well exemplified by the following image:
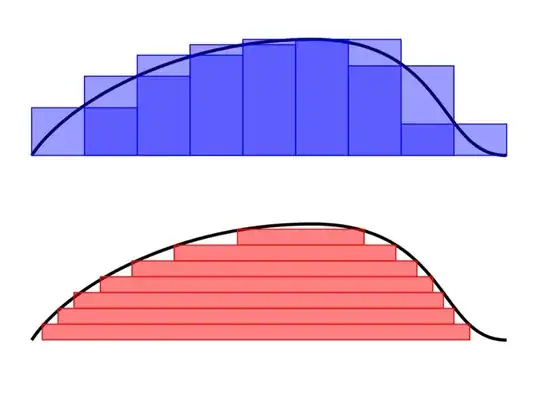
BLUE: Riemann idea. RED: Lebesgue idea

(from here let's limit ourselves to thinking only of non-negative functions for simplicity, and assuming that we know the definition of Lebesgue integral only for step function supported on measurable set)

So with Lebesgue's idea we fix a certain values $\{a_n\}, \hspace{0.2cm} a_n \in \mathbb{R^+}$ and we define $E_n=f^{-1}([0,a_n])$ and at the end we approximate the function with $f \approx \sum_n a_n \chi_{E_n}$
(Remark: This passage gives the idea but is not exactly rigorous, in fact the intersections of these steps would have to be removed, but for our discussion it is inessential)
At the end with a certain limit we Will find the rigorous definition, but is not necessary to explain for our discussion.
It is clear that in this construction it's crucial that $E_n$ had to be measurable sets, because only in these case we know how do the integral. So the class of function on which we can define the Lebesgue integral construction is the collection of f such that $E_n=f^{-1}([0,a_n])$ is a measurable set $\forall a_n \in \mathbb{R^+}$. But, with the right small adjustments, this is essentially the definition of measurable function

Another User
  • 5,048
Manuel Bonanno
  • 81