1

Can someone please explain

a) why $\log\left(\frac{z-1}{z+1}\right)$ has branch points at 1 and -1. I know what a branch point is as it is defined in my text. I've seen that sometimes we have a branch cut along the negative real axis for $log(z)$. Is there one of those as well for $\log\left(\frac{z-1}{z+1}\right)$

b) how to put $\log\left(\frac{z-1}{z+1}\right)$ into the standard complex form like how $\log(z) = \log(r) + i\theta$

enter image description here Thanks

Interstigation
  • 477
Elli
  • 91
  • 5
  • what definition of branch point are you working with? there are a few, and some are easier to work with than others. – thorimur May 08 '21 at 00:13
  • ah ok. in that case what definition of "branch cut" are you using, and do you want a formal proof, or just an intuitive one? – thorimur May 08 '21 at 00:15
  • That's very kind, I would like both if possible, if the formal one is too big than intuitive is fine. I am really struggling because I know depending upon how $\theta$ is defined $\log(z)$ can have a branch cut at any of the axis, but I can't convert this function to the format given in example 1 in the image. I am wondering as well if you could do that, and explain to me if $\log{(z-1)/(z+1)}$ is multivalued anywhere, because that's normally where branch cuts come into play. As defined in my text: a branch cut is a line used to create a domain of analyticity – Elli May 08 '21 at 00:23
  • I only had the most basic course in complex variables, so I'm guessing log(z-1)-log(z+1) has those branch points because log(z-1) has a branch point at 1 and log(z+1) has a branch point at -1, because log(z) has a branch point at 0. Something like that. Do you understand why log(z) has a branch point at z=0? – bof May 08 '21 at 00:56
  • If $z$ moves from $+i$ to $-i$ passing through $0$, then what happens to $(z-1)/(z+1)$? – Somos May 08 '21 at 01:38
  • Branch points for log are at points where the argument is zero. Here at z=1 and z=-1. – herb steinberg May 08 '21 at 03:34

1 Answers1

1

$\log$ is "always" multivalued, as $\log(x)\sim \log(x) + 2\pi i$, regardless of what $x \;(\neq 0)$ is! One question, though, is whether you always need a branch cut. One way of showing that you need a branch cut is by showing that for a family of mutually nonintersecting closed curves, the function is locally holomorphic but not possibly analytic on each of those curves. One way to do that (at least sometimes) is to phrase your function as the antiderivative of another function along those curves, and then show that the value at a given point on each of those curves is not well-defined.

That is, the integral of the derivative of $f$ around each of those curves—which should be the difference between $f$ at the beginning and end, which here are the same point, and therefore should be $0$—is actually nonzero. Here, $f(z)=\log\left(\frac{z-1}{z+1}\right)$ and $f'(z)=\frac{1}{z-1}-\frac{1}{z+1}$.

So, explicitly, for a curve $\gamma^+_{a\mapsto a}$ encircling $z=1$ but not $z=-1$, which starts and ends at $a$: $$\begin{align} 0 &= \left[\log\left(\frac{z-1}{z+1}\right)\right]_{z=a}^a \\ &= \int_{\gamma^+_{a\mapsto a}}\frac{1}{z-1}-\frac{1}{z+1}\ dz \\ &=\text{res}_{z=1}\frac{1}{z-1} - 0 \\ &=2\pi i \end{align}$$ Likewise, for a curve $\gamma^-_{a\mapsto a}$ encircling $z=-1$ but not $z=1$: $$\begin{align} 0 &= \left[\log\left(\frac{z-1}{z+1}\right)\right]_{z=a}^a \\ &= \int_{\gamma^-_{a\mapsto a}}\frac{1}{z-1}-\frac{1}{z+1}\ dz \\ &=0 - \text{res}_{z=-1}\frac{1}{z+1} \\ &=-2\pi i \end{align}$$

So, $f$ cannot be (single-valued) analytic on any domain containing such curves, lest we get a contradiction. If a (sufficiently nice) branch cut, therefore, did not include $-1$ and did not include $1$, we could arrive at a contradiction by going sufficiently close to one of those and repeating the above. So, $-1$ and $1$ need to be in every (sufficiently nice) branch cut. (There's a little more technical reasoning we could do here, but I'm guessing your text allows certain assumptions on what a "line" is or gives proof techniques for finding branch points that are a bit simpler than that would involve.)

These are the only branch points: after choosing a branch cut, we can define $\log\left(\frac{z-1}{z+1}\right)$ to be the integral of $\frac{1}{z-1}-\frac{1}{z+1}$ along some path to the point in question, plus whatever integer multiple of $2\pi i$ we like.

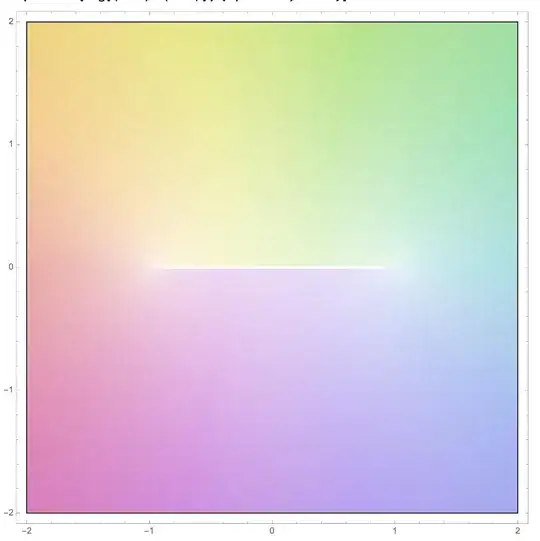
Let's construct a nice branch cut: the interval $[-1,1]$. Note that we get no contradiction by encircling the whole branch cut with a curve, since the residues cancel out. This is what we get by using the principal branch of $\log$ in our definition. Here's what $f$ looks like with that branch cut: a plot of the function above

We could also choose many other branch cuts, of course, as long as they include $-1$ and $1$ (including the branch cut with "disconnected" branches $(-\infty,-1]$, $[1,\infty)$) and as long as the resulting branch satisfies $e^{f(z_0)}=\frac{z_0-1}{z_0+1}$ at some point $z_0$.

Takeaway message: you can usually expect $\log$ to be multivalued, and to require a branch cut whenever there's a pole somewhere, since integrating the derivative around that pole will likely give you a residue.

As for getting the real and imaginary parts, it depends on your branch cut! If you use the principal branch of $\log$, you can break it up as $\log\left|\frac{z-1}{z+1}\right|+i\arg\left(\frac{z-1}{z+1}\right)$—and then if you want to simplify those in terms of $z=re^{i\theta}$, you might want to do some trig.

Let me know if anything here is unclear!

thorimur
  • 328