Rotated ellipse - calculate points with an absolute angle

Question

I can draw ellipses nicely with this formula

 alpha = 0-360 °
 x: = width * Cos (alpha)
 y: = height * Sin (alpha)

The first point (alpha = 0 °) is to the right of the center point:

and rotate the ellipse at the same time with this formula:

 alpha = 0-360 °
 beta = 20 ° inclination
 x: = width * Cos (alpha) * Cos (beta) - height * Sin (alpha) * Sin (beta)
 y: = width * Cos (alpha) * Sin (beta) + height * Sin (alpha) * Cos (beta)

Source: What is the parametric equation of a rotated Ellipse (given the angle of rotation)

When you turn, you also turn the coordinate system of the ellipse. The point alpha = 0 is now 20 ° below the center.

I'm trying to get points in the rotated ellipse with absolute angles. The green dot.

Maybe someone knows how to do it.

Answer 1

You just need to calculate the value of $\alpha$ where the ellipse crosses the positive X axis.

We have $$x = w\cos\alpha\cos\beta - h\sin\alpha\sin\beta$$ $$y = w\cos\alpha\sin\beta + h\sin\alpha\cos\beta$$

Let $y=0$ $$h\sin\alpha\cos\beta=-w\cos\alpha\sin\beta$$ $$\frac{\sin\alpha}{\cos\alpha}=\frac{-w\sin\beta}{h\cos\beta}$$ That is, $$\tan\alpha=\frac{-w}{h}\tan\beta$$

In computer code, we should use the two argument form of the arctangent function to make sure we get the correct quadrant, eg

alpha = atan2(-w*sin(beta), h*cos(beta))

So $\sin\alpha$ and $\sin\beta$ have opposite signs, and $\cos\alpha$ and $\cos\beta$ have the same sign.

Now we have to check that $x$ is positive at that $\alpha$ value. We substitute $$\sin\alpha=(-w/h) \cos\alpha\tan\beta$$ into our equation for $x$: $$x=w\cos\alpha\cos\beta - h(-w/h)\cos\alpha\tan\beta\sin\beta$$ $$x=w\cos\alpha(\cos\beta + \tan\beta\sin\beta)$$ which simplifies to $$x=w\frac{\cos\alpha}{\cos\beta}$$

Now $\cos\alpha$ and $\cos\beta$ have the same sign, so $x$ is positive, and our $\alpha$ value does, in fact, give us the point where the ellipse crosses the positive X axis.

We can now add that value as an offset to our parameter.

Let $$\delta=\arctan\left(\frac{-w\sin\beta}{h\cos\beta}\right)$$ And $$x = w\cos(\alpha+\delta)\cos\beta - h\sin(\alpha+\delta)\sin\beta$$ $$y = w\cos(\alpha+\delta)\sin\beta + h\sin(\alpha+\delta)\cos\beta$$ are our new parametric equations.

---

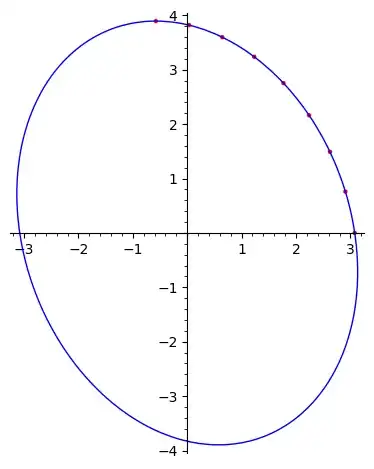
Here's some Sage / Python code that uses those equations to plot the ellipse, and several dots with $\alpha$ in the range $[0, \pi/2]$.

@interact
def main(w=3, h=4, b=20):
    b *= pi / 180
    cb, sb = cos(b), sin(b)
    d = atan2(-w * sb, h * cb)
def fx(t):
    return w * cos(t+d) * cb - h * sin(t+d) * sb

def fy(t):
    return w * cos(t+d) * sb + h * sin(t+d) * cb

P = parametric_plot([fx, fy], (0, 2*pi))
P += point([(fx(t), fy(t))
    for t in srange(0, 9*pi/16, pi/16)], color="red")
show(P)

Here's a live version, running on the SageMathCell server.

And here's the output, with the default parameters.

Here's an updated version of the script which calculates the angle of the tangent to the ellipse where it crosses the +X axis. It also draws the tangent line.

---

Note that $\alpha$, is only indirectly related to the central polar angle of the ellipse. It's actually the polar angle of the two auxiliary circles associated with this parameterization, which have radii $w$ and $h$. In astronomy, this parameter is known as the eccentric anomaly.