I'm interested if there is some hope to obtain the inverse of $$ f(t) = (1-e^{-t})t $$ for $t$ positive. If there is a formula I suspect that the Lambert W function will be involved on it. Clever approximations are also welcomed (not looking for local ones though ;).
Asked
Active
Viewed 321 times
6
-
This could be applicable. If the derivatives become manageable is as yet to be found. – Maesumi Jun 06 '13 at 10:20
-
1There certainly won't be any way to do it using just the ordinary functions of high school math. – Gerry Myerson Jun 06 '13 at 10:26
-
1Maple doesn't find the inverse in terms of the W function; it usually succeeds to find such in cases where there is an inverse involving W. – coffeemath Jun 06 '13 at 10:41
-
It is strictly increasing, so it must have an inverse. – Bunder Jun 06 '13 at 12:16
-
@Bunder Sorry, brain fart. – Did Jun 06 '13 at 12:35
-
Near $t=0$ this is $f(t) \approx t^2$ so it is not increasing or invertible. – Maesumi Jun 06 '13 at 12:56
-
To define the inverse, the function needs to be single valued, so you would have to restrict the domain of $t$ to be either $t\ge0$ or $t\le0$. The domain of the inverse function $t(f)$ is then the range of $f(t)$ which in either case is $f\ge0$. – Graham Hesketh Jun 06 '13 at 13:42
-
1@Maesumi and Graham it is for $t$ positive so the inverse is well defined. – Bunder Jun 06 '13 at 15:04
-
Ha ha woops didn't read the question properly.... – Graham Hesketh Jun 06 '13 at 16:57
2 Answers
3
For large $t$ $f(t)\sim t$, while for small t $f(t)\sim t^2$. Then for large $y$ $f^{-1}(y)\sim y$ and for small $y$ $f^{-1}(y)\sim \sqrt y$. Using this as a first approximation in Newton's method gives the following approximation: $$ f^{-1}(y)\sim h(y)=\begin{cases} \sqrt{y}-\frac{-y-e^{-\sqrt{y}} \sqrt{y}+\sqrt{y}}{e^{-\sqrt{y}} \sqrt{y}-e^{-\sqrt{y}}+1}& 0<y<1,\\ y+\frac{e^{-y} y}{e^{-y} y-e^{-y}+1}& y\ge1. \end{cases} $$ This is the graph of $f^{-1}(y)-h(y)$:
Julián Aguirre
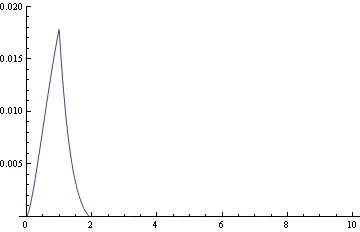
- 76,354
-
-
Given $y>0$, let $g(t)=f(t)-y$. Newton's method to solve $g(t)=0$ consists in iterating the function $N(t)=t-g(t)/g'(t)$ starting with an initial guess $t_0$. If $y<1$ take as initial guess $t_0=\sqrt y$; if $y\ge1$ take $t_0=y$. – Julián Aguirre Jun 07 '13 at 17:15
-
1
Maple does give us a series for it: if $(1-e^{-t})t = y$ and $t>0$, then $$ t = {y}^{1/2}+\frac{1}{4}\,y+{\frac {7}{96}}\,{y}^{3/2}+1/48\,{y}^{2}+{\frac {491} {92160}}\,{y}^{5/2}+{\frac {1}{960}}\,{y}^{3}+{\frac {983}{20643840}} \,{y}^{7/2}-{\frac {11}{120960}}\,{y}^{4}-{\frac {2455961}{39636172800 }}\,{y}^{9/2}-{\frac {79}{2903040}}\,{y}^{5}-{\frac {1131731179}{ 125567395430400}}\,{y}^{11/2}+\dots $$
GEdgar
- 111,679