Evaluate $\int_0^1 \sqrt\frac{1-x}{x}dx$ with the dogbone contour

Question

I'm currently working on the integral $I = \int_0^1 \sqrt\frac{1-x}{x}dx$. I would like to evaluate it with the dogbone contour specifically. Here's what I did so far:

Denote $f(z) = \sqrt\frac{1-z}{z}$ the integrand function (with complex variable). Then I observe that $$f(z) = (1 - z)^{\frac{1}{2}}z^{-\frac{1}{2}} = \frac{|1 - z|^{\frac{1}{2}}}{|z|^{\frac{1}{2}}}e^{\frac{1}{2}i(\arg(z) - \arg(1 - z))} (*)$$

Since $\ln(z) = \ln(|z|) + i\arg(z)$ (and similarly $\ln(1 - z) = \ln(|1 - z|) + i\arg(1 - z)$). Denote $Arg = \frac{1}{2}(\arg(z) - \arg(1 - z))$ for the step to come.

Next I defined $- \pi < \arg(z) \leq \pi$ and $0 \leq \arg(z) < 2\pi$, to observe the behaviour of Arg in the intervals $(- \infty, 0)$ and $(0,1)$.

• In $(- \infty, 0)$, from above, we have: $\arg(z) \to \pi$, $\arg(1 - z) \to 2\pi \implies Arg \to \frac{1}{2}(\pi - 2\pi) = - \frac{\pi}{2}$

• In $(- \infty, 0)$, from below, we have: $\arg(z) \to - \pi$, $\arg(1 - z) \to 0 \implies Arg \to \frac{1}{2}(- \pi - 0) = - \frac{\pi}{2}$

Hence we deduce that our function is continuous everywhere on this interval. However:

• In $(0,1)$, from above, we have: $\arg(z) \to 0$, $\arg(1 - z) \to 2\pi \implies Arg \to \frac{1}{2}(0 - 2\pi) = - \pi$

• In $(0,1)$, from below, we have: $\arg(z) \to 0$, $\arg(1 - z) \to 0 \implies Arg \to 0$

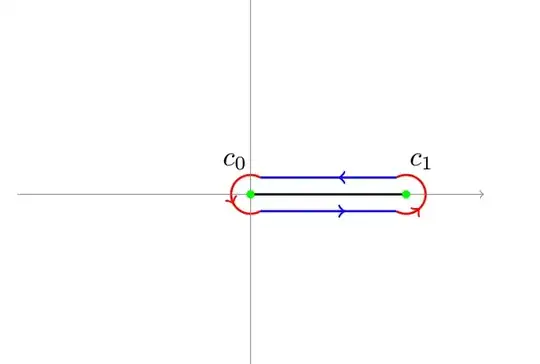
And in this interval our function is discontinuous since $e^{- i\pi} \ne e^0 = 1$. Thus I introduced a dogbone contour, namely $C$, aroud the branch $[0,1]$ such that:

$$C = \psi_1 \cup \psi_2 \cup c_0 \cup c_1$$

Where $\psi_1$ is the blue segment from $1$ to $0$ and $\psi_2$ is the blue segment from $0$ to $1$. (Thanks to @Zaid Alyafeai for the picture).

Then we have the equality: $\oint_C f(z)dz = \int_{\psi_1} f(z)dz + \int_{\psi_2} f(z)dz + \int_{c_1} f(z)dz + \int_{c_2} f(z)dz$; and pumping up $C$ we also have that $\oint_C = - 2\pi i (res_{z = 0}f(z)dz + res_{z = \infty}f(z)dz)$ by Cauchy Residue Theorem since $0,\infty$ are the only singular points of $f(z)$.

Then I computed them:

For $\int_{\psi_1} f(z)dz$ and $\int_{\psi_2} f(z)dz$, I used $z = t + i\epsilon$ with $t \in [0,1] $and $dz = dt$:

• $$\int_{\psi_1}f(z)dz = - \int_0^1\frac{(1 - t - i\epsilon)^{\frac{1}{2}}}{(t + i\epsilon)^{\frac{1}{2}}}dt = - \int_0^1 \frac{|1 - t - i\epsilon|^{\frac{1}{2}}}{|t + i\epsilon|^{\frac{1}{2}}}e^{i\pi}dt$$ (I deduced the last integral from $(*)$ and from the arguments I computed above)

Then taking the limt when $\epsilon \to 0$ I finally obtained that $\lim\limits_{\epsilon \to 0} \int_{\psi_1}f(z)dz = I$.

• In a very similar way I found that $\lim\limits_{\epsilon \to 0} \int_{\psi_2}f(z)dz = I$ as well.

Now for $\int_{c_0} f(z)dz$ and $\int_{c_1} f(z)dz$, I used $z = \epsilon e^{i\theta}$ with $\theta \in [0,2\pi]$ and $dz = i\epsilon e^{i\theta}$, and my goal was to find upper bounds of the absolute value of these integrals:

• $|\int_{c_0} f(z)dz| = |i\epsilon^{\frac{1}{2}}\int_0^{2\pi}(1 - \epsilon e^{i\theta})^{\frac{1}{2}}e^{\frac{1}{2}i\theta}dt| \leq i\epsilon^{\frac{1}{2}}\int_0^{2\pi}|1 - \epsilon e^{i\theta}|^{\frac{1}{2}}|e^{\frac{1}{2}i\theta}|dt \leq i\epsilon^{\frac{1}{2}}(1 + \epsilon)^{\frac{1}{2}}2\pi$

Thus I had: $0 \leq \lim\limits_{\epsilon \to 0}|\int_{c_0}f(z)dz[ \leq 0$ which implies that $\lim\limits_{\epsilon \to 0}\int_{c_0}f(z)dz = 0$.

In a very similar way again, I found that $\lim\limits_{\epsilon \to 0}\int_{c_1}f(z)dz = 0$.

Hence in the end I had: $\oint_Cf(z)dz = I + I + 0 + 0 = 2I$, and since I also had that $\oint_Cf(z)dz = - 2\pi i (res_{z = 0}f(z)dz + res_{z = \infty}f(z)dz)$, it follows that:

$$2I = - 2\pi i (res_{z = 0}f(z)dz + res_{z = \infty}f(z)dz) (***)$$

And that's where my problem starts (or not !): I computed both residues and found they were both equal to 0, but this implies that $I = 0$ and I feel like this is wrong, because first I don't understand why they would be 0 when looking at their shape, and second this means the "number" of $I$ on the LHS of $(***)$ does not influence our result. So I hope you can help me either finding my mistake, either to show me that those residues are not 0 because I did not achieve to find another result (either to prove me that $I = 0$ because I don't think so).

I already appreciated your time, but any help would be welcome!

Answer 1

$\DeclareMathOperator*{\res}{Res}$

I see two errors in your derivation. First you try to sum the residues at $0$ and $\infty$. This is not correct because they are in different parts of the complex plane created by your contour.

We need in fact only the residue at infinity and this appears to be not zero. The simplest way to find the residue is to expand the function into Laurent series in the annulus $|z|>1$ where the function is analytic: $$ f(z)=\sqrt\frac{1-z}z=i\sqrt{1-\frac1z}=i\left(1-\color{red}{\frac12}\frac1z-\frac18\frac1{z^2}-\cdots\right), $$ so that $$ I=\frac12\oint_C f(z)dz=-\pi i \res_{z=\infty} f(z)=-\pi i\left(\frac i2\right)=\frac\pi2. $$

---

The above value can be easily verified by real integration using substitution $x=\sin^2\theta$: $$ \int_0^1\sqrt\frac{1-x}xdx=2\int_0^{\pi/2}\cos^2\theta\,d\theta=\frac\pi2. $$

Answer 2

Are you required to use contour integration? Because there is an easier way. Let $$s=\sqrt{\frac{1-x}{x}}\iff x=\frac{1}{s^2+1}\implies \mathrm{d}s=\frac{-2u}{(1+s^2)^2}~\mathrm{d}s$$ So $$\int_0^1 \sqrt{\frac{1-x}{x}}\mathrm{d}x=\int_{\infty}^0s~\frac{-2s}{(1+s^2)^2}\mathrm{d}s$$ $$=\int_0^\infty \frac{2s^2}{(1+s^2)^2}\mathrm{d}s$$ Now you can integrate by parts. Let $$u=s,\mathrm{d}u=\mathrm{d}s$$ $$\mathrm{d}v=\frac{2s}{(1+s^2)^2}\mathrm{d}s\implies v=\frac{-1}{s^2+1}$$ Where the last bit follows from a simple substitution $t=s^2$. So, $$\int_0^\infty u~\mathrm{d}v=(uv)\big|^{s=\infty}_{s=0}-\int_0^\infty v~\mathrm du$$ $$=\left(\frac{-s}{s^2+1}\right)\bigg|^\infty_0+\int_0^\infty \frac{1}{1+s^2}\mathrm{d}s$$ And I'm sure you know the last integral by heart! The first term vanishes and we are left simply with $$\int_0^1\sqrt{\frac{1-x}{x}}\mathrm{d}x=\int_0^\infty \frac{1}{1+s^2}\mathrm{d}s=\frac{\pi}{2}$$

Answer 3

An easier way is: \begin{align} \int_0^1\sqrt{\dfrac{1-x}{x}}dx&=\frac12\int_0^1\frac{2-2x}{\sqrt{x(1-x)}}dx\\&=\frac12\left(\int_0^1\frac{1-2x}{\sqrt{x-x^2}}dx+\int_0^1\frac{1}{\sqrt{(\frac12)^2-(x-\frac12)^2}}dx\right)\\ &=\frac12\left(2\sqrt{x-x^2}\Bigg|_0^1+\left.\sin^{-1}\left(\frac{x-\frac12}{\frac12}\right)\right|_0^1\right)\\ &=\boxed{\frac\pi2} \end{align}