4

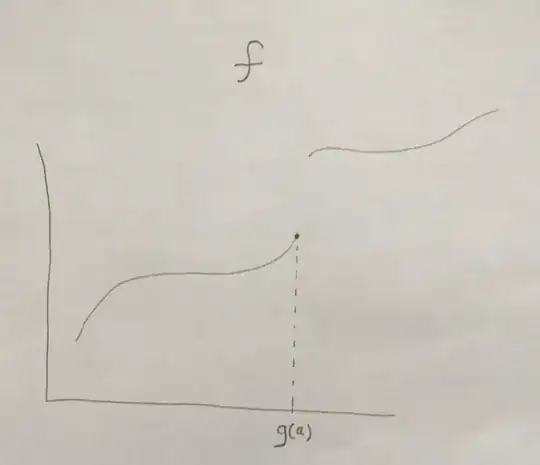
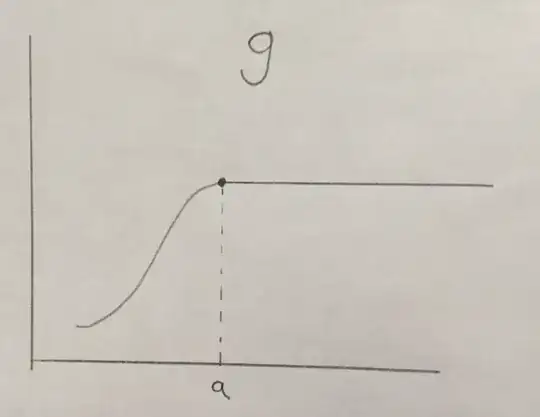
I've been playing around with the limits of compositions...e.g. $\displaystyle \lim_{x \to a}(f \circ g) (x)$...and wanted to confirm my intuition that just because $\displaystyle \lim_{x \to a}(f \circ g) (x)=L$, it is not necessarily the case that $\displaystyle \lim_{x \to g(a)}f(x)=L$.

Said differently, if $\displaystyle \lim_{x \to a}(f \circ g) (x)=L$, then we cannot generally conclude that $\displaystyle \lim_{x \to g(a)}f(x)=L$.

The pictures (hand drawn, sorry) I had in mind are the following:

f graph g graph

where the function $g$ maintains its value for all $x \geq a$.

The definition of $\displaystyle \lim_{x \to a}(f \circ g) (x)=L$, which is $\forall \epsilon \gt 0 \exists \delta \gt 0 \forall x \in \mathbb R \big [ 0 \lt \lvert x -a \rvert \lt \delta \rightarrow \lvert (f \circ g)(x) - L \rvert \lt \epsilon \big ] $ for $L = f(g(a))$, seems to be satisfied. From the graph of $f$, clearly $\displaystyle \lim_{x \to g(a)}f(x)\neq f(g(a))$.

Is this the correct intuition?

S.C.
  • 4,984
  • Related. – Giuseppe Negro May 04 '21 at 11:22
  • "then we cannot generally conclude that $\lim_{x\to a}f(x) = L.$" Did you mean $f(g(a))$ as you mention in the end of your question? – Giorgos Giapitzakis May 04 '21 at 11:24
  • @GiorgosGiapitzakis Good catch: I think I edited correctly to remove any ambiguity. – S.C. May 04 '21 at 11:26
  • 1
    Your intuition is correct. See this related question. For a more formal proof see the second answer. – Giorgos Giapitzakis May 04 '21 at 11:30
  • @GiuseppeNegro I am not experienced enough to make a lot of sense out of your post, but I am assuming that my $g$ here is functioning as a "path". In which case, your post suggests that I can make no conclusions regarding the behavior of $f$ near the point $g(a)$ (which seems to be in line with my above statements). Is that correct? – S.C. May 04 '21 at 11:39
  • 1
    See also here, specifically the last part "Limit Substitutions without continuity, basic gist" https://math.stackexchange.com/a/3982790/754927 or a more concise take here https://math.stackexchange.com/a/1073047/754927 – Ben May 04 '21 at 14:37
  • 1
    @scramer: yes, that is correct, that's more or less what I was hinting at. That other post of mine is not exactly the same, though, it is multidimensional and considers the problem of taking "all" paths. So ignore it if it confuses you. – Giuseppe Negro May 06 '21 at 11:59

1 Answers1

1

To grasp the concept, just take $g(x)=G$ a constant function.

When determining the limit $\lim\limits_{x\to a}f(g(x))=\lim\limits_{x\to a}f(G)=f(G)$ you can see clearly that the neighbourhood of $a$ is not even involved since $g$ is not varying.

It is therefore impossible to deduct the local behaviour of $f$ from a single value.

It suffice then to take $f$ discontinuous at $G$ so that $\lim\limits_{x\to G}f(x)$ is not defined.

This is an extreme example, but it illustrates where the problem originates.

Similarly imagine you have $g$ positive and want to study the limit of $f$ at $0$. The problem is despite $g$ being well behaved (continuous and all) since it takes only positive values, at most you can only get information for $f$ in $0^+$ and there is no way to know what happen on the left side in $0^-$ and furthermore determine the status of $\lim_{x\to 0}f(x)$.

  • take for instance $f(x)=\lfloor x\rfloor$ and $g(x)=x^2$ then $f\circ g\to f(0^+)=0$ but $f(0^-)=-1$
zwim
  • 28,563