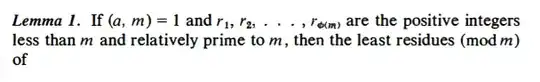For context, this lemma is later used to prove that $1 \equiv a^{\phi(m)}$ (mod $m$). However, I don't understand why $r_j$ is the least residue of $ar_i$ for some $i$ and $j$ in $[1, \phi(m)]$. The proof seems to imply that this follows from the fact that $ar_i$ is relatively prime to $m$, but I don't understand the reasoning. Simple explanations if possible, my background is high school math and a bit of self study.
I must say, though. The theorems in number theory are quite beautiful.
If $\gcd(a,m) = 1$, by Bezout's identity, there are integers $x$ and $y$ such that $ax + my = 1$. Notice that this says $ax \cong 1 \pmod{m}$, so $x$ is a multiplicative inverse of $a$ modulo $m$.
Using Bezout's identity in reverse looks like "given $a$ and $b$, if there are integers $u,v$ such that $au+bc = d$, then $\gcd(a,b)$ divides $d$." If that $d = 1$, then $\gcd(a,b) = 1$ and $a$ is relatively prime to $b$.
why $r_j$ is the least residue of $ar_i$ for some $i$ and $j$ in $[1,\phi(m)]$
(fixed that typo right at the end for you.)
Let $i \in [1,\phi(m)]$. Since $r_i$ is relatively prime to $m$, Bezout's identity gives an $x_i$ such that $x_i r_i \cong 1 \pmod{m}$. Then $(ax)(r_ix_i) \cong 1\cdot 1 \cong 1 \pmod{m}$.
We can rearrange $(ax)(r_ix_i)$ to obtain $$ (ar_i)(xx_i) \cong 1 \pmod{m} \text{.} $$
But, using Bezout's identity in reverse, that means $\gcd(a r_i,m) = 1$, so $ar_i$ is relatively prime to $m$. Therefore $ar_i$ is congruent to one of $r_1, \dots, r_{\phi(m)}$ modulo $m$.
If $(a,m)=1$, then $a$ is invertible $\pmod m$. This implies easily that the map given by left multiplication by $a$ on $\mathbb Z_m^\times$ is invertible. Hence it's a bijection.
That left multiplication by $a$ is a bijection of $\mathbb Z_m^\times$ follows from the second part, since as is clearly demonstrated (using Euclid's lemma, without calling it that), $(ar_i,m)=1$ for each $i$.
Hence the equivalence classes of the $ar_i$ are the $\phi(m)$ distinct elements of $\mathbb Z_m^\times$.