This question was asked in INMO 2005 and here is the problem:
Let $(a,b)$ $\in$ $\mathbb{N}$ $s.t$
$\cfrac{43}{197}$ $\lt$ $\cfrac{a}{b}$ $\lt$ $\cfrac{17}{77}$. $\text{Find}$ $\min(b)$.
My first approach to this question was to take reciprocal of the fractions.
If the numbers have different integral part then I pick the middle term to be the smallest positive integer. But I don't know how to continue. Any hint or help is appreciated
Thanks
This can be done simply by a binary search using Farey mediants. The idea is as follows: given an interval $(a/b,c/d)$ containing our fractions we compare them to the mediant "midpoint" $\,m = (a+c)/(b+d).\,$ If they are both less then $m$ then we replace the upper bound $c/d$ by $m$. If the are both greater then $m$ we replace the lower bound $\,a/b\,$ by $m$. Else $m$ lies between them, and by basic properties of Farey sequences it is the fraction with least denominator between them.
We start with the containing interval $(0/1, 1/0) = (0,\infty).\,$ Its mediant $\,(0\!+\!1)/(1\!+\!1) = 1/1\,$ exceeds both so our new upper bound is $\color{#f60}{1/1}$. The mediant of $\,0/1,1/1$ is $1/2$ which still exceeds so $\color{#0af}{1/2}$ is our new upper bound. This continues till we reach upper bound $\color{#90f}{1/4}$ which then yields a mediant $\,(0\!+\!1)/(1\!+\!4)=\color{#c88}{1/5}$ which is smaller than both, so our new interval is $(1/5,1/4)$ Continuing this way yields the sequence below, till we reach $\,\color{#0a0}{7/32}\,$ between them.
$$\dfrac{0}1 < \color{#c88}{\dfrac{1}5} < \dfrac{3}{14}< \dfrac{5}{23} < \!\!\underbrace{\color{#c00}{\dfrac{43}{197}} < \color{#0a0}{\dfrac{7}{32}} < \color{#c00}{\dfrac{17}{77}}}_{\!\!\!\approx\ \color{#c00}{0.21827}< \color{#0a0}{0.21875} < \color{#c00}{0.22078}}\!\!\!<\dfrac{2}9 < \color{#90f}{\dfrac{1}4} < \dfrac{1}3 < \color{#0af}{\dfrac{1}2}<\color{#f60}{\dfrac{1}1}<\dfrac{1}0\qquad $$
Remark $ $ Note that the mediant $\,\frac{a}b\oplus \frac{c}d = \frac{a+c}{b+d}\,$ can be viewed geometrically as the slope of the diagonal of a parallelogram with sides of slope $a/b$ and $c/d$ formed by the vectors $(b,a)$ and $(d,c),\,$ which makes its "intermediate" property intuitively clear geometrically, i.e. the diagonal lies between the sides, as illustrated below.
$\quad$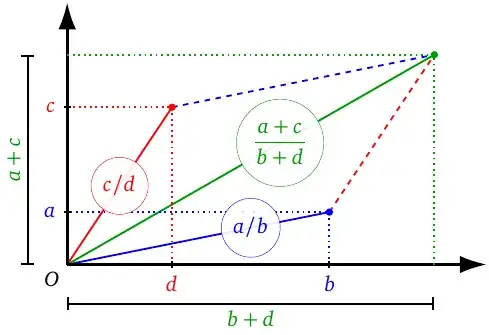 
This simple mediant property is used in many places, e.g. the classical proof of irrationality of $\sqrt 2$. It is a simple example of various geometric (lattice theoretic) methods that often lead to beautiful geometric proofs of number theoretical results (e.g. a key property of Farey sequences can be proved using Pick's area theorem as here).
Properties of Farey mediants and sequences are proved in most textbooks on elementary numbers theory, usually in sections on best rational approximation or continued fractions.
Your approach seem to be implicitly using an equivalent approach using continued fractions, e.g. compare this answer where I show how to compare real numbers by computing their continued fractions in parallel. In fact there are many equivalent views of these manifestations of the Euclidean algorithm (see also the Stern-Brocot tree and diatomic sequences) which all prove enlightening depending on the context.
You can solve this by using the method of continued fractions given on Wikipedia. I find this to be the best method unless you want to do something like The one used in (Q2) INMO 2005
The continued fraction for $43/197$ is $[0;4,1,1,2,1,1,3]$ while for $17/77$ it is $[0;4,1,1,8]$, so the ‘best rational’ between them would be either $$ [0;4,1,1, \min\{(8,2)+1\}] = 7/32 $$ or $$ [0;4,1,1,\min(8,2)] = 5/23 $$ (see this answer if you are confused about why I took two cases).
Now clearly, $5/23$ doesn’t lie in the interval so $7/32$ is your answer.
